特徵超曲面

特徵超曲面(characteristic hypersurface)是求解雙曲型方程或研究其解的性質時起重要作用的一種超曲面。

基本介紹

• 中文名：特徵超曲面
• 外文名：characteristic hypersurface
• 領域：數學
• 學科：曲面
• 性質：一種超曲面
• 方程：雙曲型方程

概念

特徵超曲面(characteristic hypersurface)是求解雙曲型方程或研究其解的性質時起重要作用的一種超曲面。一個超曲面S：φ(t，x)=0，如果在其上成立：

就稱S是方程：

的一個特徵超曲面，其中：

稱為方程(1)在(x，t)處的特徵方程。對於雙曲型方程，任一特徵超曲面均由雙特徵線組成，而雙特徵線(又稱特徵射線)t=t(τ)，x=x(τ)由如下常微分方程組：

滿足附加條件(2)的解給出。由過一點P(t⁰，x⁰)的一切雙特徵線所構成的特徵超曲面，稱為以P為頂點的特徵劈錐面，特徵劈錐面連同其內部稱為特徵劈錐體，它們由位於t≥t和t≤t的向前及向後兩部分組成。過P點指向此劈錐面內部的任一方向，稱為此點的類時方向；一個處處和類時方向相切的曲線稱為時向曲線。以P為頂點的特徵劈錐內部的任一點，都可用時向曲線與P點相連結。對曲面上任一點，都有經過該點且位於此曲面上的時向曲線時稱此曲面為時向曲面。處處將劈錐的前後兩部分分隔開的超曲面稱為空向曲面。對方程(1)，超曲面(t=常數)就是空向曲面。對波動方程，雙特徵線都是直線x_i=a_i+α_it(i=1，2，…，n)，式中：

而以P(t，x)為頂點的特徵劈錐面就是特徵錐面：

此時t軸恰為一個時向曲線。在方程(1)的主部的係數有界時，以任何點為頂點的特徵劈錐面都可包含在以此點為頂點的一個固定大小的圓錐中。解的弱間斷面一定是特徵超曲面。因此，在波的傳播中，特徵超曲面可用來表示波前，即作為已受擾動與未受擾動的區域的分界面，而任何擾動都沿著雙特徵線傳播。

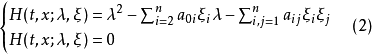
擾動沿雙特徵線傳播的性質，充分體現了一般情形下線性雙曲型偏微分方程的解的奇性傳播的特點。在光學中，雙特徵線就是光線，沿著它們積分一些常微分方程，在高頻振動的情形下，可得到精確解的漸近展開式。此方法稱為幾何光學近似。它將波動光學和幾何光學聯繫起來，並為傅立葉積分運算元提供了一個雛型。

雙曲型微分方程

雙曲型偏微分方程是描述振動或波動現象的一類重要的偏微分方程。雙曲型偏微分方程解可以分解為振動與振動相乘，或指數函式與指數函式相乘的形式，一般能量無窮。

雙曲型偏微分方程簡稱雙曲型方程，是偏微分方程的一種類型。它主要用於描述振動、波動現象與相應的運動過程。它的一個典型特例是波動方程和n=1時的波動方程。可用來描述弦的微小橫振動，稱為弦振動方程。這是最早得到系統研究的一個偏微分方程。

對於非線性雙曲型方程，雙曲型的定義一般要依賴於所考察方程的解。非線性雙曲型方程柯西問題光滑的存在性一般只能是局部的。它的解在有限時間內會產生奇性。