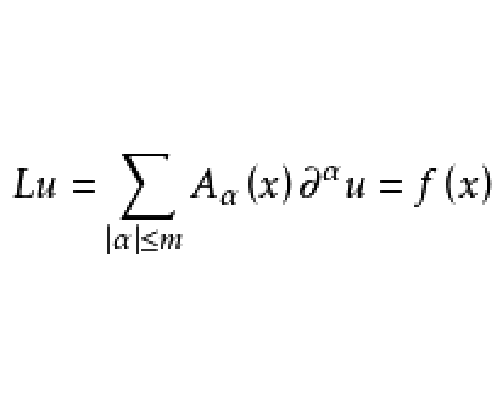次特徵帶(bicharacteristic strip)又名雙特徵帶,是偏微分方程理論中的一個概念。對於一般的m階線性偏微分運算元P(x,Dx) ,這裡P(x,Dx)是的多項式,其象徵為P(x,ξ),主象徵為Pm(x,ξ)。為了方便,記t為x0,x= (x0,x1,...,xn)相應於以上結果是:對於超曲面有如果一個超曲面φ(x)=0(grad φ≠0)適合,則稱它是P的特徵超曲面。如果在(x,ξ)空間考慮,並視ξ為一向量,(x,ξ)就成為x空間中x點處的接觸元素。這樣,其解將稱為P的次特徵帶,它在x空間的投影稱為次特徵曲線。一切適合於一定條件的特徵超曲面都是由次特徵曲線“織”成的。
基本介紹
- 中文名:次特徵帶
- 外文名:bicharacteristic strip
- 所屬學科:數學
- 屬性:偏微分方程理論中的一個概念
- 相關概念:特徵,特徵帶,微局部分析等
基本介紹,相關概念,特徵(曲線),哈密頓-雅可比方程,
基本介紹








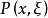
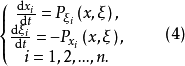

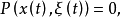

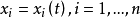
相關概念
特徵(曲線)


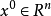







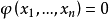


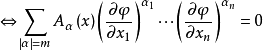



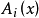

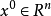


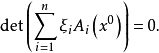




哈密頓-雅可比方程
哈密頓-雅可比方程(Hamilton-Jacobi equation)是不含未知函式本身的一階非線性方程的特徵微分方程組,在分析力學、幾何學、變分學,特別是偏微分方程的特徵理論中常常遇到不顯含未知函式本身的一階非線性偏微分方程