光程函式方程(eikonal equation)一類重要的一階非線性偏微分方程。
如果一階非線性方程

的解可用隱函式抓二;,xZ, ..,二。,u)=0給出,則可得到方程
它可以形式地被視為n }--1個自變數(}xl,xz,"..,x
, u)的不顯含獷的一階非線性方程.如果從中解出某一個偏導數,例如a列au,且把形式的偏微分方程
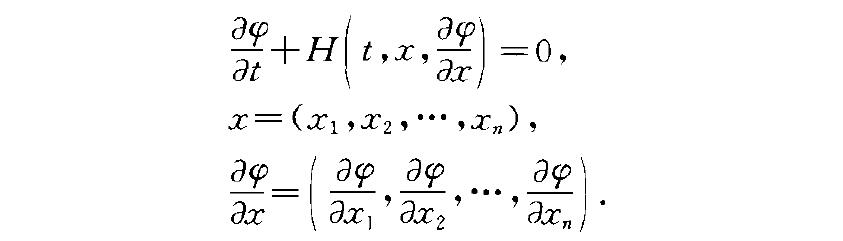
這樣的方程稱為一階偏微分方程的標準型,也稱為哈密頓一雅可比方程.在幾何光學中稱為光程函式方程.
光程函式方程(eikonal equation)一類重要的一階非線性偏微分方程。

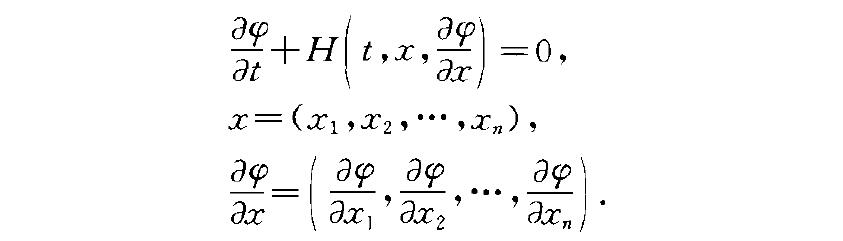
光程函式方程(eikonal equation)一類重要的一階非線性偏微分方程。... 光程函式方程(eikonal equation)一類重要的一階非線性偏微分方程。如果一階非線性方程...
光程函式 S滿足哈密頓-雅可比方程哈密頓方程組是變分積分或的歐拉-拉格朗日方程,若哈密頓函式不顯含 x ,則 H 是運動常量,即沿任何解u(x),H 是常數。 [1]...
,xn(s),p1(s),p2(s),…,pn(s))≡0的雙特徵帶稱為零雙特徵帶,一階偏微分方程的標準型也稱為哈密頓-雅可比方程(參見“光程函式方程”) [2] 。
,xn(s),p1(s),p2(s),…,pn(s))≡0的雙特徵帶稱為零雙特徵帶,一階偏微分方程的標準型也稱為哈密頓-雅可比方程(參見“光程函式方程”) [3] 。
