哈密頓方程組(Hamilton system)是與歐拉-拉格朗日方程組等價的一階微分方程組。
基本介紹
- 中文名:哈密頓方程組
- 外文名:Hamilton system
- 適用範圍:數理科學
簡介


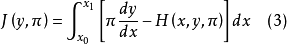
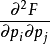


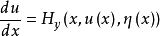
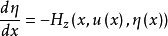
性質



哈密頓方程組(Hamilton system)是與歐拉-拉格朗日方程組等價的一階微分方程組。


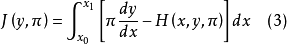
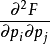


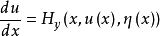
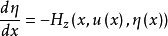



哈密頓方程組(Hamilton system)是與歐拉-拉格朗日方程組等價的一階微分方程組。...... 哈密頓方程組(Hamilton system)是與歐拉-拉格朗日方程組等價的一階微分方程組...
經典力學中一組描寫系統運動的一階微分方程組。是W.R.哈密頓於1834年提出的,又稱哈密頓方程或正則方程。...
在物理學裡,哈密頓-雅可比方程 (Hamilton-Jacobi equation,HJE) 是經典力學的一種表述。哈密頓-雅可比方程、牛頓力學、拉格朗日力學、哈密頓力學,這幾個表述是互相...
哈密頓量是一個物理辭彙,是系統的能量算符,是一個描述系統總能量的算符,以H表示。哈密頓量在大部分的量子理論公式中十分重要。...
哈密頓-雅可比-貝爾曼方程(Hamilton-Jacobi-Bellman equation,簡稱HJB方程)是一個偏微分方程,是最優控制的核心。HJB方程式的解是針對特定動態系統及相關代價函式下,有...
又稱典型系統或正則系統或哈密頓典型系統(方程),常簡記為H.S.。在對映射函式適當的要求之下,證明了2維點映射不變閉曲線存在,從而得到太陽系是穩定的結論,這是...
哈密頓-雅可比-貝爾曼-埃薩克斯方程(Hamil-ton-Jacobi-Bellman-Isaacs equation)微分對策問題中一種基本方程...
哈密頓原理,是英國數學家W.B.哈密頓1834年發表的動力學中一條適用於完整系統十分重要的變分原理。它可表述為:在N+1維空間(q1,q2,…,qN;t)中,任兩點之間...
量子力學中,哈密頓算符(Hamiltonian) H為一個可觀測量(observable),對應於系統的的總能量。一如其他所有算符,哈密頓算符的譜為測量系統總能時所有可能結果的集合...
威廉·哈密頓爵士(Sir William Rowan Hamilton,1805年8月4日-1865年9月2日),愛爾蘭數學家、物理學家及天文學家。哈密頓最大的成就在於發現了四元數,並將之...
在廣義相對論中,哈密頓-雅可比-愛因斯坦方程(英語:Hamilton–Jacobi–Einstein equation,簡稱HJEE)是一道哈密頓形式、描述超空間中的幾何力學的方程。創於“幾何力學...
從數學形式上,就是將麥克斯韋方程組的積分形式化為微分形式。倒三角形為哈密頓運算元。注意:(1)在不同的慣性參照系中,麥克斯韋方程組有同樣的形式。...
哈特里方程是指把多電子原子中的多電子的波函式近似寫成各單粒子波函式的乘積,對相互作用多電子哈密頓量運用變分原理可以導出哈特里方程。...
《完全可積非線性方程的哈密頓理論》是2006年科學出版社出版的圖書,作者是黃念寧,本書對弧子理論中研究的特別活躍的幾種方程:NLS方程,KdV方程,UNLS方程,DNLS方程...
哈密爾頓-雅戈比方程是分析力學中用以求解正則方程的一個偏微分方程 。哈密頓-雅可比方程Hamilton-Jacobi equation由CGJ雅可比在W.R.哈密頓研究工作基礎上給出而得名...
在數學中,馬蒂厄方程是用於處理套用數學中各種問題的某些特殊功能,包括:振動橢圓...精確的平面波解決方案在廣義相對論中、量子擺哈密頓函式的本徵函式、旋轉電偶極...
這樣的方程稱為一階偏微分方程的標準型,也稱為哈密頓一雅可比方程.在幾何光學中稱為光程函式方程. [1] 參考資料 1. 數學辭海第3卷 詞條標籤: 科學 ...
雅可比定理(Jacobi theorem)是用哈密頓-雅可比方程解哈密頓方程組的一個方法。...... 雅可比定理(Jacobi theorem)是用哈密頓-雅可比方程解哈密頓方程組的一個方法。...
關於哈密頓正則方程組的解的穩定性理論﹐這種理論是科爾莫戈羅夫(Andrey Nikolaevich Kolmogorov,1903年4月25日-1987年10月20日)﹑阿爾諾德(Vladimir Igorevich ...
正則變換是由一組正則變數到另一組能保持正則形式不變的變數的變換。在哈密頓力學裡,正則變換(canonical transformation)是一種正則坐標的改變,(q,p)-->(Q,P)...
