基本介紹
- 中文名:拉格朗日函式
- 外文名:Lagrangian Function
- 提出者:約瑟夫·拉格朗日
- 領域:數學,物理學等
- 別稱:拉格朗日量
定義




概念

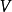



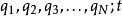
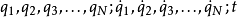



























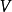



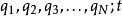
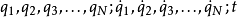





















在數學最優問題中,拉格朗日乘數法(以數學家約瑟夫·路易斯·拉格朗日命名)是一種尋找變數受一個或多個條件所限制的多元函式的極值的方法。這種方法將一個有n 個...
拉格朗日函式是在力學繫上只有保守力的作用,是描述整個物理系統的動力狀態的函式。...... 拉格朗日函式是在力學繫上只有保守力的作用,是描述整個物理系統的動力狀態的...
基本的拉格朗日乘子法就是求函式f(x1,x2,...)在約束條件g(x1,x2,...)=0下的極值的方法。其主要思想是將約束條件函式與原函式聯立,從而求出使原函式取得...
約瑟夫·拉格朗日(Joseph Louis Lagrange),法國數學家、物理學家。他在數學、力學和天文學三個學科領域中都有歷史性的貢獻,其中尤以數學方面的成就最為突出。...
描述流體運動的兩種方法之一。拉格朗日法又稱隨體法:跟隨流體質點運動,記錄該質點在運動過程中物理量隨時間變化規律。拉格朗日法是以研究單個流體質點運動過程作為基礎...
在數學中的最最佳化問題中,拉格朗日乘數法(以數學家約瑟夫·拉格朗日命名)是一種尋找多元函式在其變數受到一個或多個條件的約束時的極值的方法。這種方法可以將一個有...
拉格朗日中值定理又稱拉氏定理,是微分學中的基本定理之一,它反映了可導函式在閉區間上的整體的平均變化率與區間內某點的局部變化率的關係。拉格朗日中值定理是羅...
剛體在重力作用下,繞旋轉對稱軸上的定點轉動(拉格朗日陀螺)的歐拉動力學方程的解,對三體問題的求解方法有重要貢獻,解決了限制性三體運動的定型問題。拉格朗日對流體...
拉格朗日量(又稱拉格朗日函式)是動能T 與勢能V 的差值:L=T-V。通常,動能的參數為廣義速度 q'1,q'2……q'N (符號上方的點號表示對於時間t的全導數),而...
約瑟夫·拉格朗日(Joseph-Louis Lagrange,1736~1813)全名為約瑟夫·路易斯·拉格朗日,法國著名數學家、物理學家。1736年1月25日生於義大利都靈,1813年4月10日卒於...
拉格朗日力學,分析力學中的一種,由拉格朗日在1788年建立,是對經典力學的一種的新的數學表述。經典力學,最初的表述形式由牛頓建立,它著重分析位移,速度,加速度,力...
基本的拉格朗日乘子法(又稱為拉格朗日乘數法),就是求函式 f(x1,x2,...) 在 g(x1,x2,...)=0 的約束條件下的極值的方法。其主要思想是引入一個新的...
從數學意義上,最優控制過程可分為三類:拉格朗日問題、麥耶爾問題和波爾扎問題。如果已知系統的狀態方程與初始狀態,要求最優控制u(t),使得相應的積分型指標為極小,...
在數值分析中,拉格朗日插值法是以法國十八世紀數學家約瑟夫·拉格朗日命名的一種多項式插值方法。許多實際問題中都用函式來表示某種內在聯繫或規律,而不少函式都只能...
拉格朗日括弧法國數學家和力學家 J.-L.拉格朗日研究正則變換時所用的一種數學符號。拉格朗日括弧是一種與泊松括弧關係密切的運算,1808年至1810年間由約瑟夫·拉格朗日...
拉格朗日定理存在於多個學科領域中,分別為:微積分中的拉格朗日中值定理;數論中的四平方和定理;群論中的拉格朗日定理 (群論)。...
拉格朗日密度即拉格朗日量,實質為從粒子體系推廣到場體系的自然對應。在分析力學裡,一個動力系統的拉格朗日量(英語:Lagrangian),又稱為拉格朗日函式,是描述整個物理系統...
拉格朗日反演(Lagrange,1770)給出了解析函式的逆的冪級數表示,建立了函式方程和冪級數乘積之間的聯繫。...
拉格朗日差分法(Lagrangian difference methods)一類偏微分方程數值解法.指利用拉格朗日坐標,從拉格朗日形式流體力學方程出發求解流體力學問題的差分方法的總稱,簡稱拉格朗日...
拉格朗日插值公式(外文名Lagrange interpolation formula)指的是在節點上給出節點基函式,然後做基函式的線性組合,組合係數為節點函式值的一種插值多項式。...
拉格朗日(行星運動)方程(Lagrangeplane-tary equation )是一種行星受攝運動的方程。...
對三變數函式F(x, y, λ) = f(x, y) + λg(x, y)...這樣求極值的方法就叫做拉格朗日乘數法、λ叫做拉格朗日乘數。V百科往期回顧 詞條...
y(x)在條件及邊界條件之下,給泛函以極值,且若y(x)是滿足條件的泛函J的平穩函式,則存在這樣一個常數λ,使y(x)是泛函的平穩函式,常數λ稱為歐拉-拉格朗日常數...
