基本介紹
- 中文名:全導數
- 外文名:Total derivative
- 本質:作為一類導數概念的補充
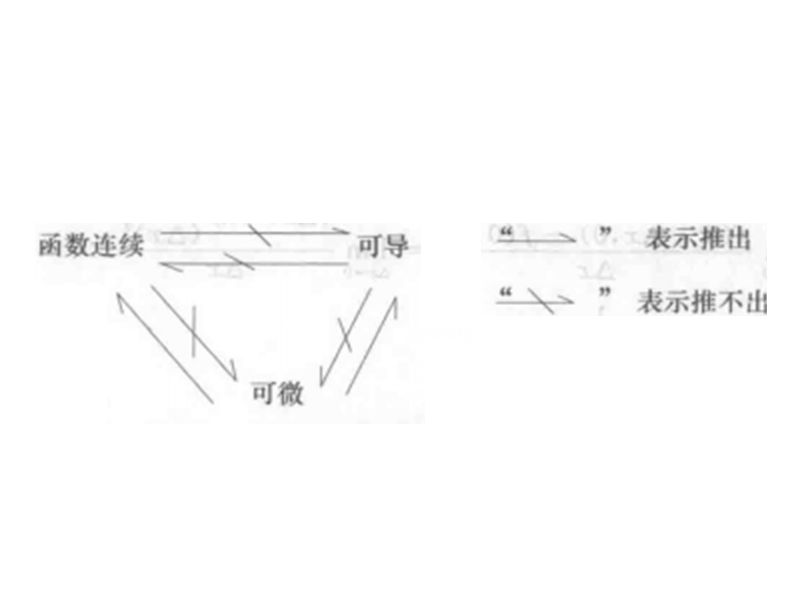
- 特別注意:二元函式連續、可導、可微的關係
- 重要定理:各種鎖鏈法則
- 套用學科:高等數學
定義,相關定理,一一型鎖鏈法則,二一型鎖鏈法則,三一型鎖鏈法則,典例,例1,例2,
定義
設z是u、v的二元函式z=f(u,v),u、v是x的一元函式u=u(x)、v=v(x),z通過中間變數u、v構成自變數x的複合函式。這種兩個中間變數、一個自變數的多元複合函式是一元函式,其導數稱為全導數。
相關定理
一一型鎖鏈法則
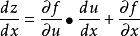
二一型鎖鏈法則

證明:對於自變數x的該變數△x,變數u=u(x)、v=v(x)的改變數△u,△v,進一步有函式的該變數△z,因為函式z=f(u,v)可微,即有

對上式左右兩端同除△x,得到:

又因為u=u(x)、v=v(x)可導,當 時,對上式左右兩端同時取極限,則有:
時,對上式左右兩端同時取極限,則有:


至此,證明完畢。
三一型鎖鏈法則
在中間變數多於兩個時,如z=f(u,v,w),而u=u(x)、v=v(x)、w=w(x),類似可得三一型全導數鎖鏈法則,即:
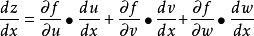
典例
例1
解:由二一型全導數鎖鏈法則,計算得到:

例2

解:外層函式顯含自變數s,由一一型全導數鎖鏈法則,計算得到: