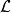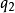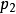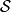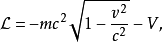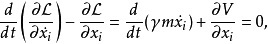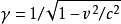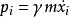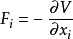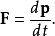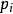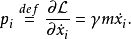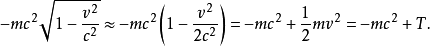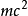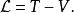拉格朗日量密度

拉格朗日密度即拉格朗日量，實質為從粒子體系推廣到場體系的自然對應。

在分析力學里，一個動力系統的拉格朗日量（英語：Lagrangian），又稱為拉格朗日函式，是描述整個物理系統的動力狀態的函式，對於一般經典物理系統，通常定義為動能減去勢能。

在分析力學里，假設已知一個系統的拉格朗日量，則可以將拉格朗日量直接代入拉格朗日方程，稍加運算，即可求得此系統的運動方程。

拉格朗日量是因數學家和天文學家約瑟夫·拉格朗日而命名。

基本介紹

• 中文名：拉格朗日量密度
• 外文名：Lagrangian (field theory)
• 實質：從粒子體系到場體系的自然對應
• 別稱：拉格朗日量

概念

拉格朗日量定義

拉格朗日量是動能T與勢能V的差值：

通常，動能的參數為廣義速度 （符號上方的點號表示對於時間{\displaystyle t}的全導數），而勢能的參數為廣義坐標 ，所以，拉格朗日量的參數為 。解析一個問題，最先要選擇一個合適的廣義坐標。然後，計算出其拉格朗日量。假定這些參數（廣義坐標、廣義速度）都互相獨立，就可以用拉格朗日方程來求得系統的運動方程。

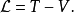
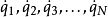
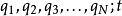
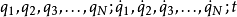
假設一個物理系統的拉格朗日量為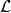，則此物理系統的運動，以拉格朗日方程表示為

其中， 是時間， 是廣義坐標， 是廣義速度。

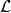
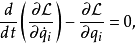
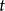
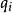
拉格朗日量與作用量的關係

一個物理系統的作用量 是一種泛函，以數學方程定義為

其中，是系統的拉格朗日量，廣義坐標是時間的函式，和分別為初始時間和終結時間。

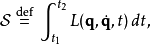
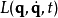
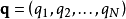
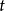
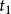
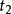
假若，作用量的一次變分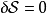，作用量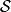為平穩值，則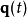正確地描述這物理系統的真實演化。從這變分運算，可以推導出拉格朗日方程

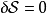
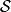
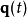
詳盡相關導引，請參閱拉格朗日方程。

拉格朗日表述

重要性

拉格朗日表述是經典力學的一種重新表述。拉格朗日表述的重要性，不只是因為它可以廣泛套用在經典力學；而更是因為它能夠幫助物理學家更深刻地了解一個物理系統的物理行為。雖然拉格朗日只是在尋找一種表述經典力學的方法，他用來推導拉格朗日方程的平穩作用量原理，已被學術界公認為在量子力學也極具功用。

優點

• 拉格朗日表述不會被任何坐標系統捆綁住。拉格朗日表述使用廣義坐標來描述系統的空間參數。它所涉及的物理量是動能與勢能，這些物理量的值不會隨廣義坐標的選擇而改變。因此，對於系統的種種約束，可以選擇一組最合適的廣義坐標，來計算問題的解答。
  
• 拉格朗日表述能夠簡易地延伸至其他學術領域。電路學、量子力學、粒子物理學、等等，都可以用拉格朗日表述來分析。
  
• 如果用同樣的表述可以分析不同學術領域的物理系統，這些系統必定有結構上的類推。在一個學術領域的新發現，意味著很可能在另一個學術領域會有類似的現象。
  

可略坐標和守恆定律

拉格朗日量有一個優良的性質，那就是守恆定律可以很容易地從它的表達式讀出來。例如，假設拉格朗日量跟某廣義速度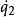有關，而跟廣義坐標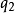無關，則對應的廣義動量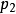是一個守恆量。這種坐標稱為“可略坐標”，或“循環坐標”。更詳細地說，拉格朗日量的形式為

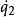
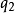
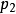
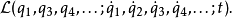
直接檢視，就可以發覺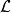跟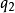無關，因此可以推斷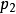是一個守恆量。

以此類推，假設，時間不在的表達式裡面，則哈密頓量守恆，即能量守恆。這種物理行為是諾特定理的一個特別案例。

檢驗粒子的拉格朗日量

假定檢驗粒子的質量和電荷超小，其對於外在系統的影響可以忽略。檢驗粒子時常可以想像為簡單的質點粒子，只擁有質量和電荷性質。像電子或上夸克一類的真實粒子具有更複雜的性質，它們的拉格朗日量含有更多項目。

在狹義相對論的四維空間裡，一個移動中的粒子的相對論性拉格朗日量可以寫為

其中，m是粒子的靜質量，c是光速，v是粒子的速度。

其拉格朗日方程為

其中，是洛倫茲因子。

注意到動量、作用力。將這些公式代入拉格朗日方程，就可複製牛頓第二定律的方程：

因此，這拉格朗日量被認定為正確無誤。

這粒子的廣義動量定義為

假設這物理系統的勢能為零，這粒子是自由粒子，則此系統的能量函式h為

這是質能方程：粒子的總能量等於其質量乘以光速平方。

假設粒子速度超小於光速，則拉格朗日量的動能部分可以近似為

靜質量的能量是個常數，可以忽略（其變分等於零）。相對論性拉格朗日量又變回經典拉格朗日量：

參見

• 哈密頓量
  
• 哈密頓原理
  
• 拉格朗日力學
  
• 哈密頓力學