基本介紹
定義

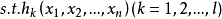
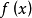
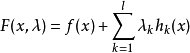
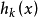
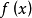
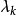
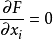
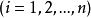
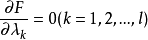
基本原理
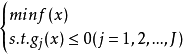
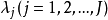
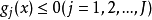
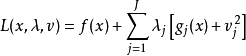
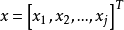
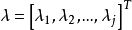
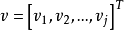
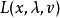
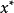
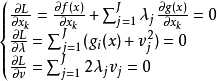
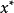
計算過程
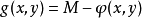
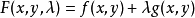
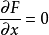
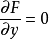
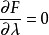
關鍵參數含義
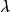
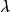
直觀意義
引理一
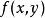
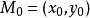
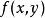

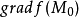
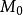
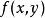
引理二
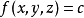
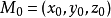
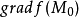
定理

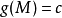
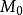
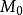
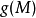
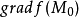
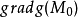
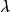
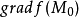
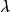
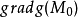
部分套用
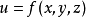
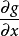
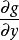
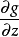
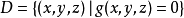
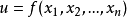
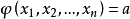
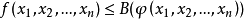
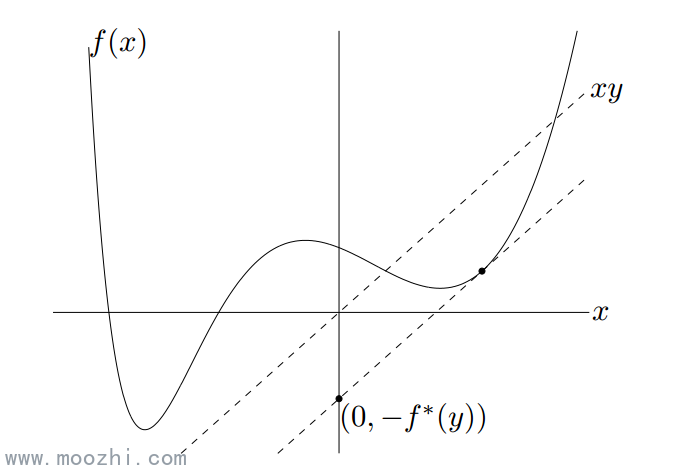

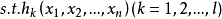
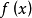
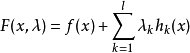
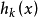
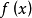
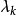
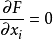
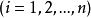
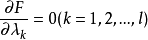
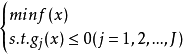
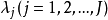
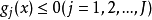
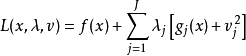
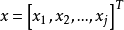
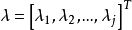
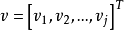
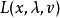
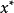
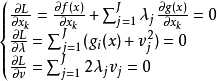
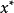
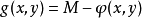
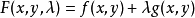
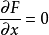
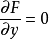
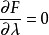
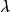
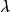
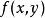
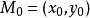
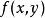

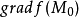
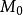
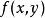
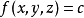
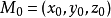
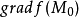

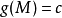
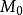
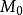
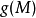
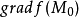
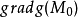
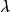
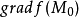
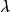
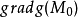
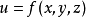
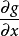
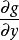
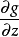
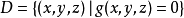
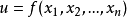
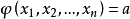
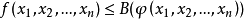
在數學最優問題中,拉格朗日乘數法(以數學家約瑟夫·路易斯·拉格朗日命名)是一種尋找變數受一個或多個條件所限制的多元函式的極值的方法。這種方法將一個有n 個...
基本的拉格朗日乘子法就是求函式f(x1,x2,...)在約束條件g(x1,x2,...)=0下的極值的方法。其主要思想是將約束條件函式與原函式聯立,從而求出使原函式取得...
基本的拉格朗日乘子法(又稱為拉格朗日乘數法),就是求函式 f(x1,x2,...) 在 g(x1,x2,...)=0 的約束條件下的極值的方法。其主要思想是引入一個新的...
乘子法( multiplier method)約束極小化的算法。對於約束極小化問題(NP):min.廠(x)s.t.廳,(』)=O(J=l,…,研)。其中XE尺“。經典的拉格朗日乘子法是...
在數學中的最最佳化問題中,拉格朗日乘數法(以數學家約瑟夫·拉格朗日命名)是一種尋找多元函式在其變數受到一個或多個條件的約束時的極值的方法。這種方法可以將一個有...
廣義乘子法(generalised method of multipli-ers)一種求解約束非線性規劃問題的方法.即把古典的拉格朗日乘子法與外點法結合起來求最優解的方法.在懲罰因子M適當大...
時,泛克里金與普通克里金的無偏估計條件等價,因此普通克里金可以視為泛克里金的一個特例。將上式作為拉格朗日乘子可得泛克里金的求解系統 [1] :將...
目前求解接觸問題常用的算法有罰函式法和拉格朗日乘子法,這2 種方法的共同點是將有約束條件的變分問題轉化為無約束條件的變分問題求解。拉格朗日乘子法是通過在...
作為一種最佳化算法,拉格朗日乘子法主要用於解決約束最佳化問題,它的基本思想就是通過引入拉格朗日乘子來將含有n個變數和k個約束條件的約束最佳化問題轉化為含有(n+k)個...
邊界條件將影響近似解函式形式的選擇,強加約束條件可通過拉格朗日乘子法被變分方程所吸收。另一方面,泛函取駐定值的變分方程對應有泛函積分式中被積函式對其變元的...
約束最最佳化問題(constrained optimization problem)是指具有約束條件的非線性規劃問題。僅有等式約束條件的約束最最佳化問題,可採用消元法、拉格朗日乘子法或罰函式法,將...
LM是拉格朗日乘子法的縮寫 LM也是“天黑請閉眼”(遊戲)中平民(亂民)的簡稱。[1] LM是lady gaga的冬粉的稱謂:little monster(小怪獸) lm系列積體電路,如lm317...
拉格朗日乘數法是求約束極值的一種方法,其基本思想是引進參數,把約束極值問題化為無約束極值問題。設需要求目標函式f:E( Rn)→R在約束條件gi(x)=0(gi:E→R,...
其中λ為拉格朗日乘子對分別對拉格朗日函式每個變數求偏導並令其值為0,解出 ...對於約束條件比較簡單的條件極值,還可以使用代入法將其化為無條件極值.即從前述...
他先後提出了零件可靠性設計的拉格朗日乘子法以及摩擦傳動的可靠性理論,並廣泛套用於礦井提升機事故治理、摩擦傳動可靠性分析等重要工程領域,獲得成功,取得了顯著的...
6.4.3 普通拉格朗日乘子NP方法的神經網路6.4.4 增廣拉格朗日乘子方法的神經網路習題參考文獻第7章 用神經網路解決矩陣代數問題7.1 概述...
1957至1976年,從事飛機顫振、潛艇龍骨設計、化工管板設計、氧氣頂吹的轉爐爐蓋設計、大型電機零件設計、高能電池、三角級數求和,以及變分原理中拉格朗日乘子法的研究...
增加了爆炸模擬中常用的歐拉描述的控制方程(含非守恆形式和守恆形式),擴展了應力率內容並給出了其Lie 導數解釋,補充了接觸算法的增廣拉格朗日子乘子法,擴充了接觸...
對於只有等式約束的非線性規劃,經典的拉格朗日乘子法指出,在對函式加以一定限制下,最優解可在一組函式方程的解集中去尋求,但是並未指出行之有效的算法。1951年,H...
