正文,
正文
泛函的數學意義是函式空間對數值空間的某種確定的映射關係,泛函定義域中的每一種可取函式對應一個確定的泛函值。通常,泛函具有含可取函式()(及其導函式)的定積分的形式
(1)
式中表示維空間的積分變數(,,…,,…,);是維積分區域;是以,媉/媉,…為變元的函式式。
電磁場問題中不少具有明確物理意義的工程參量可以表示為未知場函式的泛函,例如分立導體與之間的電容量是導體表面電荷函式()或導體之間電位函式()的泛函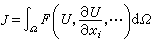 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法
電磁場問題中不少具有明確物理意義的工程參量可以表示為未知場函式的泛函,例如分立導體與之間的電容量是導體表面電荷函式()或導體之間電位函式()的泛函
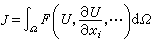 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法(2)
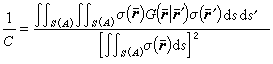 電磁場的泛函法
電磁場的泛函法(3)
式中是以導體表面()和()為邊界的場域,是場域中媒質的介電常數,(│′)是以′為源點和為場點的電位格林函式,線積分路徑()可取任意起迄於()和()的連續曲線。又如,波導的傳播常數或電磁諧振腔的諧振頻率都是電場函式和(或)磁場函式的泛函;天線的輸入導抗或散射物體的散射截面都是其電流函式的泛函等。
電磁場問題由未知場函式的方程(微分方程、積分方程等)和定解條件所組成,按泛函的觀點可抽象為運算元方程的形式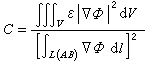 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法
電磁場問題由未知場函式的方程(微分方程、積分方程等)和定解條件所組成,按泛函的觀點可抽象為運算元方程的形式
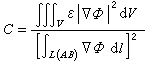 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法(4)
式中是未知函式的定義域,是內的已知函式;Γ是的邊界,g是Γ上的已知函式;是方程運算元,是邊界條件運算元。問題的近似解與準確解之差為誤差函式,經運算元和分別映射為方程的和邊界條件的餘量函式和。餘量函式說明解在整個定義域上的近似程度,由於它們實際上不可能恆等於零(否則就是準確解),只能按某種平均意義來衡量。通常取近似解餘量函式的某種加權內積值作為評價其準確性的誤差泛函。
電磁場問題中的這兩類泛函──參量值的泛函和誤差泛函,分別對應於兩類求解方法,即變分法和加權餘量法,統稱為泛函法。
40年代,物理學家J.S.施溫格首先將變分法引入電磁波的散射和繞射問題。變分法的泛函方程又稱變分方程,是使泛函的一階變分等於零=0,即泛函式對可取函式取駐定值(穩定值)。電磁場問題中的各種物理原理(能量原理、最小作用量原理和反應原理等)往往能說明某些參量的泛函值具有駐定性,其可取函式必須取能使泛函為駐定值(包括極大或極小值的情況)的形式,從而使這些參量與電磁場未知函式歸結成統一的求解內容。例如,根據靜電場最小儲能的湯姆遜定理,可知式(2)和(3)的泛函都應為極小值,據此可同時求解電容量和電荷函式或電位函式,根據所得1/和的近似值(略大於準確值)可判斷其誤差。
此外,抽象為運算元方程的數學模型還可轉化為等價的變分方程,使變分法可以直接用於求解方程的未知函式。例如,確定性運算元方程的等價關係為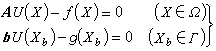 電磁場的泛函法
電磁場的泛函法
電磁場問題中的這兩類泛函──參量值的泛函和誤差泛函,分別對應於兩類求解方法,即變分法和加權餘量法,統稱為泛函法。
40年代,物理學家J.S.施溫格首先將變分法引入電磁波的散射和繞射問題。變分法的泛函方程又稱變分方程,是使泛函的一階變分等於零=0,即泛函式對可取函式取駐定值(穩定值)。電磁場問題中的各種物理原理(能量原理、最小作用量原理和反應原理等)往往能說明某些參量的泛函值具有駐定性,其可取函式必須取能使泛函為駐定值(包括極大或極小值的情況)的形式,從而使這些參量與電磁場未知函式歸結成統一的求解內容。例如,根據靜電場最小儲能的湯姆遜定理,可知式(2)和(3)的泛函都應為極小值,據此可同時求解電容量和電荷函式或電位函式,根據所得1/和的近似值(略大於準確值)可判斷其誤差。
此外,抽象為運算元方程的數學模型還可轉化為等價的變分方程,使變分法可以直接用於求解方程的未知函式。例如,確定性運算元方程的等價關係為
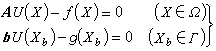 電磁場的泛函法
電磁場的泛函法(5)
(6)
式中是線性下有界運算元,是待定本徵值,變分方程(6)中兩個內積之比稱為瑞利商。根據電磁場問題的具體物理條件和性質,變分方程可以附有或不附有邊界條件和強加約束條件。邊界條件將影響近似解函式形式的選擇,強加約束條件可通過拉格朗日乘子法被變分方程所吸收。另一方面,泛函取駐定值的變分方程對應有泛函積分式中被積函式對其變元的某種微分方程,稱為該變分方程的歐拉微分方程。凡歐拉微分方程在所給邊界條件下的解必定是使所對應的泛函值駐定的可取函式。
變分法的求解過程分為間接法和直接法兩類。早期所用的間接法是先將變分方程轉化為它的歐拉微分方程後再求解;直接法則有正交函式系展開法、有限差分法和里茲法等。套用最普遍的是稱作里茲法的直接法。
加權餘量法作為運算元方程的一類近似解法的概括,包含有伽略金法(1915)、子域法(1923)、最小二乘法(1928)、狹義的矩量法(1932)和配置法(1937)等獨立發展的解法,它們都有相似的求解過程,使近似解餘量在各種平均意義下的誤差泛函值等於零。R.F.哈林頓(1967)將這些方法引入電磁場邊值問題並稱之為(廣義的)矩量法。解運算元方程的伽略金法與所對應的解變分方程的里茲法完全等價,而且是矩量法中收斂性最好的一種選擇。
在泛函法的近期發展中,還將有限差分的思想加入到變分法或加權餘量法中,相繼出現了有限元法(1960)、邊界元法(1967)和單矩法(1974)等複合泛函法。
選取某一與線性無關的完備的函式 序 列{()|}作為基函式序列,構成方程的近似解的序列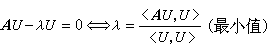 電磁場的泛函法
電磁場的泛函法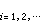 電磁場的泛函法
電磁場的泛函法
變分法的求解過程分為間接法和直接法兩類。早期所用的間接法是先將變分方程轉化為它的歐拉微分方程後再求解;直接法則有正交函式系展開法、有限差分法和里茲法等。套用最普遍的是稱作里茲法的直接法。
加權餘量法作為運算元方程的一類近似解法的概括,包含有伽略金法(1915)、子域法(1923)、最小二乘法(1928)、狹義的矩量法(1932)和配置法(1937)等獨立發展的解法,它們都有相似的求解過程,使近似解餘量在各種平均意義下的誤差泛函值等於零。R.F.哈林頓(1967)將這些方法引入電磁場邊值問題並稱之為(廣義的)矩量法。解運算元方程的伽略金法與所對應的解變分方程的里茲法完全等價,而且是矩量法中收斂性最好的一種選擇。
在泛函法的近期發展中,還將有限差分的思想加入到變分法或加權餘量法中,相繼出現了有限元法(1960)、邊界元法(1967)和單矩法(1974)等複合泛函法。
選取某一與線性無關的完備的函式 序 列{()|}作為基函式序列,構成方程的近似解的序列
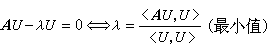 電磁場的泛函法
電磁場的泛函法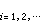 電磁場的泛函法
電磁場的泛函法(7)
式中{|}是待求的線性組合係數。於是泛函的駐定值問題=0就轉化為多變數函式的極值問題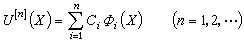 電磁場的泛函法
電磁場的泛函法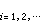 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法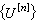 電磁場的泛函法
電磁場的泛函法
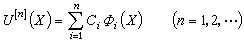 電磁場的泛函法
電磁場的泛函法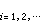 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法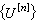 電磁場的泛函法
電磁場的泛函法(8)
由此解出{}後即得級近似解()。對於線性運算元方程的等價變分方程,所得的式(8)為線性代數方程組,例如對確定性方程(5),可得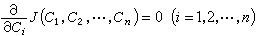 電磁場的泛函法
電磁場的泛函法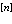 電磁場的泛函法
電磁場的泛函法
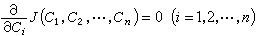 電磁場的泛函法
電磁場的泛函法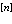 電磁場的泛函法
電磁場的泛函法(9)
對本徵值方程(6),可得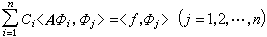 電磁場的泛函法
電磁場的泛函法
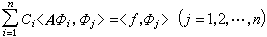 電磁場的泛函法
電磁場的泛函法(10)
式中為本徵值的級近似解。根據基函式序列的完備性,取得越大則近似解的準確性越好,且收斂於準確解。
當變分方程附有第一類齊次邊界條件時,要求基函式序列都符合齊次邊界條件(變分方程不必滿足第二類或第三類邊界條件)。若附有第一類非齊次條件,則應先將它歸入方程的未知函式而維持邊界條件的齊次性。
選取基函式序列同變分法。另選取線性無關的權函式序列{()|},將它們依次對方程的餘量函式作內積,使所得誤差泛函都等於零。即有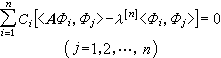 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法
當變分方程附有第一類齊次邊界條件時,要求基函式序列都符合齊次邊界條件(變分方程不必滿足第二類或第三類邊界條件)。若附有第一類非齊次條件,則應先將它歸入方程的未知函式而維持邊界條件的齊次性。
選取基函式序列同變分法。另選取線性無關的權函式序列{()|},將它們依次對方程的餘量函式作內積,使所得誤差泛函都等於零。即有
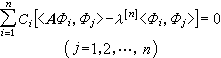 電磁場的泛函法
電磁場的泛函法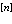 電磁場的泛函法
電磁場的泛函法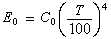 電磁場的泛函法
電磁場的泛函法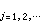 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法(11)
對於線性運算元方程,所得的式(11)亦為線性代數方程組。例如,對確定性方程(5),可得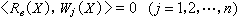 電磁場的泛函法
電磁場的泛函法
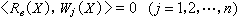 電磁場的泛函法
電磁場的泛函法(12)
對本徵值方程(6),可得 電磁場的泛函法
電磁場的泛函法
 電磁場的泛函法
電磁場的泛函法(13)
隨著的增大,近似解也收斂於準確解。
當{()}={()},即權函式序列與基函式序列相同的加權餘量法稱為伽略金法,顯然與里茲法等價。子域法以矩形脈衝函式為權;配置法以-函式為權;狹義的矩量法以冪函式序列 {|}作為權函式序列;最小二乘法則以餘量函式對待求係數的變化率作為權函式的復共軛。另一方面,基函式序列也有各種不同的選擇,用得較多的是矩形脈衝函式、三角脈衝函式、分段正弦函式等分域基函式;有時也用多項式全域基函式。
若選取的基函式嚴格滿足所給的方程,但近似符合邊界條件,則從邊界條件的餘量函式出發同樣能建立加權餘量法的方程組,並據以求得問題的近似解。這類解法稱為邊界積分法。
利用有限差分法的概念,將加權餘量法的子域未知函式表示成離散結點上未知函式取樣值的多項式插值函式,就發展成有限元法(當子域為整個場域的一部分時)或邊界元法(當子域為場域邊界的一部分時)。單矩法在實質上是數學邊界上的邊界元法與界內的有限元法(或有限差分法),以及界外的分離變數法三者的聯合。 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法
當{()}={()},即權函式序列與基函式序列相同的加權餘量法稱為伽略金法,顯然與里茲法等價。子域法以矩形脈衝函式為權;配置法以-函式為權;狹義的矩量法以冪函式序列 {|}作為權函式序列;最小二乘法則以餘量函式對待求係數的變化率作為權函式的復共軛。另一方面,基函式序列也有各種不同的選擇,用得較多的是矩形脈衝函式、三角脈衝函式、分段正弦函式等分域基函式;有時也用多項式全域基函式。
若選取的基函式嚴格滿足所給的方程,但近似符合邊界條件,則從邊界條件的餘量函式出發同樣能建立加權餘量法的方程組,並據以求得問題的近似解。這類解法稱為邊界積分法。
利用有限差分法的概念,將加權餘量法的子域未知函式表示成離散結點上未知函式取樣值的多項式插值函式,就發展成有限元法(當子域為整個場域的一部分時)或邊界元法(當子域為場域邊界的一部分時)。單矩法在實質上是數學邊界上的邊界元法與界內的有限元法(或有限差分法),以及界外的分離變數法三者的聯合。
 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法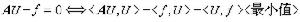 電磁場的泛函法
電磁場的泛函法 電磁場的泛函法
電磁場的泛函法