由區域內的已知場源和邊界上的物理狀況,通過麥克斯韋方程組求解區域內電磁場的問題。
基本介紹
- 中文名:電磁場的邊值問題
正文
靜場情形 對於靜電場,基本方程歸結為靜電勢()的泊松方程
變化電磁場情形 對於隨時間變化的電磁場,常將和用矢量勢(,)和標量勢(,)表出
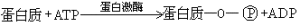 電磁場的邊值問題
電磁場的邊值問題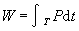 電磁場的邊值問題
電磁場的邊值問題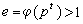 電磁場的邊值問題
電磁場的邊值問題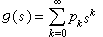 電磁場的邊值問題
電磁場的邊值問題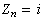 電磁場的邊值問題
電磁場的邊值問題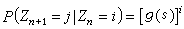 電磁場的邊值問題
電磁場的邊值問題電磁場方程是線性的,可將電磁場分解為各種頻率的單色(單頻率)場的線性疊加即傅立葉級數或傅立葉積分,從而只需著重研究單色場
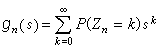 電磁場的邊值問題
電磁場的邊值問題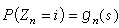 電磁場的邊值問題
電磁場的邊值問題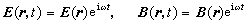 電磁場的邊值問題
電磁場的邊值問題方程(7)是矢量方程。如果用笛卡兒坐標,則()和()的各分量分別滿足標量亥姆霍茲方程
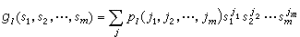 電磁場的邊值問題
電磁場的邊值問題解的唯一性 數學上可以證明,泊松方程(1)或拉普拉斯方程在前述邊界條件下的解是惟一的,電勢有時可以相差一無關緊要的常數。如果場源局限於有限區域而求解區域伸展至無限遠,邊界條件還要求。
拉普拉斯方程在零邊界條件下的惟一解是零解。亥姆霍茲方程有所不同,存在一系列數(=1,2,3,…)使得方程在零邊界條件下有非零解,這些和稱為該邊值問題的本徵值和本徵函式,相應的電磁振盪稱為本徵模式。一般的振盪是這些本徵模式的線性疊加,疊加係數根據初始條件決定;在實際的套用中,則往往用適當的激勵方式,使得只有特定模式被激勵。
只要不等於,亥姆霍茲方程在邊界條件
(,,已知)下的解是惟一的。對於伸展至無限遠的區域,還要加上索末菲輻射條件
常用的求解方法有鏡像法。還有分離變數法,即對於某個正交坐標系來說,在邊界形狀比較規則的情況下,把偏微分方程分解成常微分方程,從而求出用本徵函式展開成無窮級數的解。還有格林函式法,即在一定條件下,尋找附加了邊界條件的微分運算元的反運算元的積分核,進而求得積分形式解析解。此外,還有將某些邊界條件較複雜的平面標量場轉化為邊界形狀較簡單的平面標量場的保角變換法等。以上這些方法都受邊界形狀和場域介質的限制,用它們可以求得解析解的電磁場邊值問題很有限,在很多情況下需要依靠數值解法。數值解法很多,如差分法;在一定邊值條件下求某泛函極值的里茲法;以及由里茲法和伽遼金法發展而來的有限元法等。
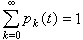 電磁場的邊值問題
電磁場的邊值問題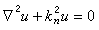 電磁場的邊值問題
電磁場的邊值問題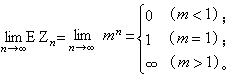 電磁場的邊值問題
電磁場的邊值問題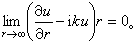 電磁場的邊值問題
電磁場的邊值問題