基本介紹
- 中文名:哈密頓原理
- 外文名:Hamilton's principle
- 別名:最小作用原理
- 提出人:W.B.哈密頓
- 提出時間:1834年
- 所屬領域:物理學
定義
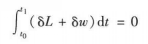
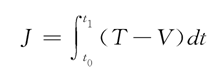
如同一般變分原理一樣,從哈密頓原理可以等價地推出相應的質點組的運動方程,通常是微分方程.如果力學系統處於靜力平衡穩定狀態,則因動能為零,位能與時間無關,哈密頓原理轉化為最小位能原理:
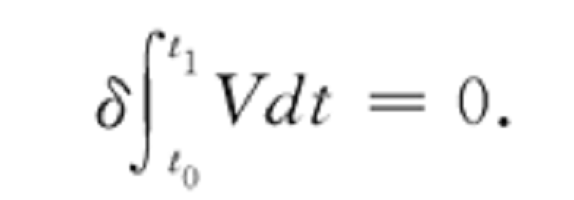
原理驗證
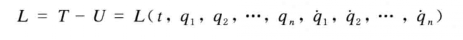 式1
式1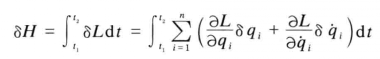 式2
式2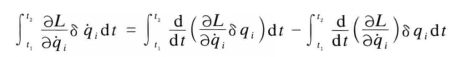 式3
式3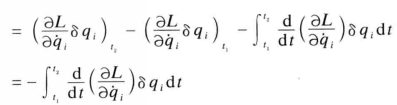 式3
式3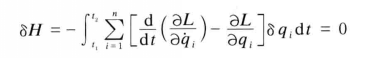
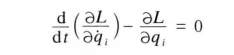 式5
式5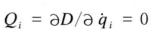
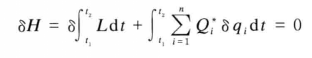 式6
式6



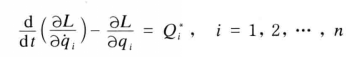 式7
式7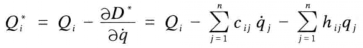 式9
式9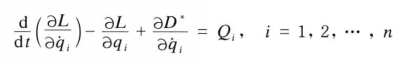
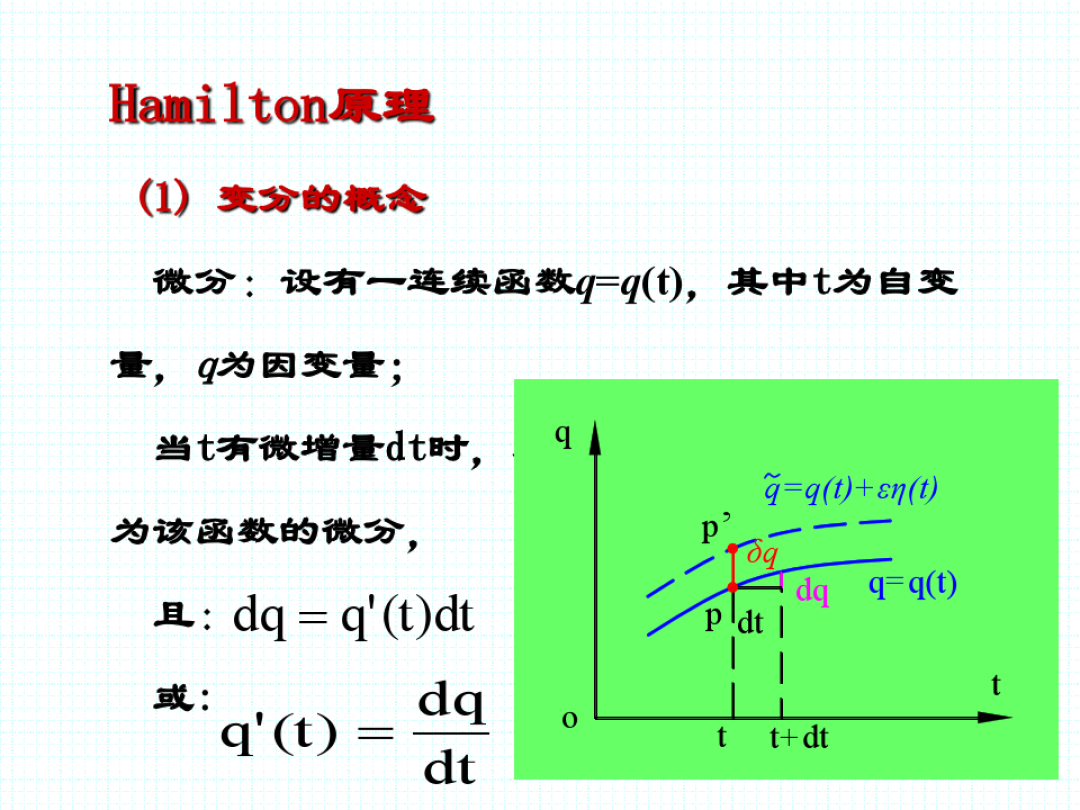
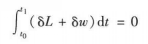
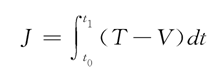
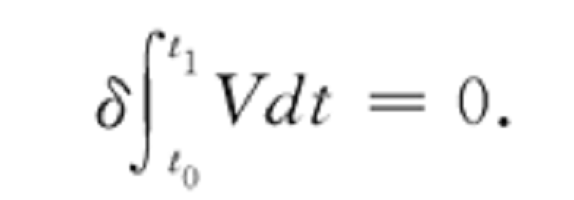
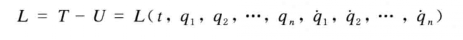 式1
式1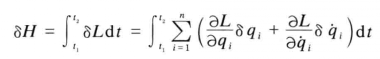 式2
式2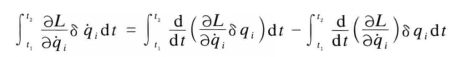 式3
式3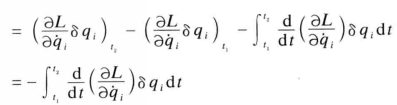 式3
式3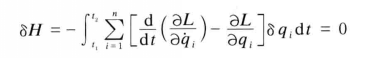
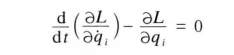 式5
式5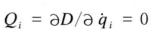
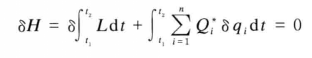 式6
式6



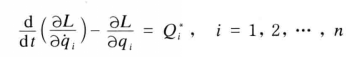 式7
式7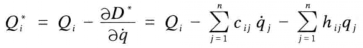 式9
式9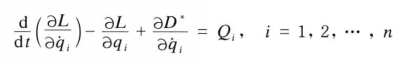
哈密頓原理,是英國數學家W.B.哈密頓1834年發表的動力學中一條適用於完整系統十分重要的變分原理。它可表述為:在N+1維空間(q1,q2,…,qN;t)中,任兩點之間...
哈密頓(William Rowan Hamilton 1805~1865) 英國數學家,物理學家,力學家。1805年8月4日生於愛爾蘭都柏林;1865年9月2日卒於愛爾蘭都柏林。...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。哈密頓群(Hamilton group)是一類非交換群。若H不是阿貝爾群,H的每個...
哈密頓圈多面體(Hamiltonian circuit polytope)是一種特殊的多面體。它是由哈密頓圈導出的多面體。它的頂點相應一個圖上的哈密頓圈的鄰接矩陣。...
最小作用量原理有很多種例子,主要的例子是莫佩爾蒂原理(Maupertuis' principle)和哈密頓原理。 在最小作用量原理之前,有很多類似的點子出現於測量學和光學。古埃及...
關於數學描述、推導和實用方法,請參閱條目作用量。最小作用量原理有很多種例子,主要的例子是莫佩爾蒂原理(Maupertuis' principle)和哈密頓原理。...
在物理學裡,哈密頓-雅可比方程 (Hamilton-Jacobi equation,HJE) 是經典力學的一種表述。哈密頓-雅可比方程、牛頓力學、拉格朗日力學、哈密頓力學,這幾個表述是互相...
費馬原理(Fermat's principle)最早由法國科學家皮埃爾·德·費馬在1662年提出:光...費馬原理參閱 編輯 費馬 哈密頓原理 最小作用量原理 路徑積分表述 惠更斯...
哈密頓原理(應該就是上文的漢密爾頓原理)是分析力學中的一條公理,無法再用更基本的理論推導出,其正確性只能由其解決的問題來證明。...
諾特定理和量子力學深刻相關,因為它僅用經典力學的原理就可以認出和海森堡測不準...經典力學上,哈密頓表述中,M是一個一維流形R,代表時間而目標空間是廣義位置的...
在該表述中,粒子穿過所有可能的始態和終態的所有路徑;特定終態的機率是所有可能導向它的軌跡的機率之和。在經典力學的範圍,路徑積分表述簡單的退化為哈密頓原理。...
故牛頓力學可稱為矢量力學;拉格朗日體系和哈密頓體系所著重的量是系統的能,它具有標量的性質,可以通過力學的變分原理建立系統的動力學方程,故拉格朗日體系和哈密頓...
即以對哈密頓原理進行修正得到的最大流原理為基礎,對開放的複雜系統建立新的統計系綜,構造出新的勢函式,並推導出隨機動力學方程,進而得出重整化方程並進行求解,...
1. 變質量經典系統的哈密頓原理和諾特定理 .中國知網.1985-04-02[引用日期2016-11-19] 2. 物理學中的宇稱守恆定律和其它對稱定律 .中國知網.1958-01-31[引用...
1.2.2 準坐標下的哈密頓原理1.2.3 阿佩爾方程1.3 連續系統的拉格朗日方程1.3.1 離散系統到連續系統的過渡1.3.2 連續系統拉格朗日方程的建立...
卡羅需-庫恩-塔克條件:拉格朗日乘數的推廣。 拉格朗日方程式 哈密頓原理 作用量 參考資料 1. Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). "...
