哈密頓圈多面體(Hamiltonian circuit polytope)是一種特殊的多面體。它是由哈密頓圈導出的多面體。它的頂點相應一個圖上的哈密頓圈的鄰接矩陣。
基本介紹
- 中文名:哈密頓圈多面體
- 外文名:Hamiltonian cycle polytope
- 領域:數學
- 性質:一種特殊的多面體
- 概念:由哈密頓圈導出
- 命名:哈密頓
概念,哈密頓圈問題,哈密頓圖,哈密頓,
概念
哈密頓圈多面體(Hamiltonian circuit polytope)是一種特殊的多面體。它是由哈密頓圈導出的多面體。它的頂點相應一個圖上的哈密頓圈的鄰接矩陣。因為任何一個圖G的哈密頓多面體均為與G同階的完全圖Kn(n為G的階)的哈密頓多面體的一個面,所以通常所說的哈密頓多面體均指完全圖的哈密頓多面體。這時,Kn的哈密頓圈的集合與如下的方程和不等式組解集確定的多面體整頂點的集合之間有一個一一對應關係:
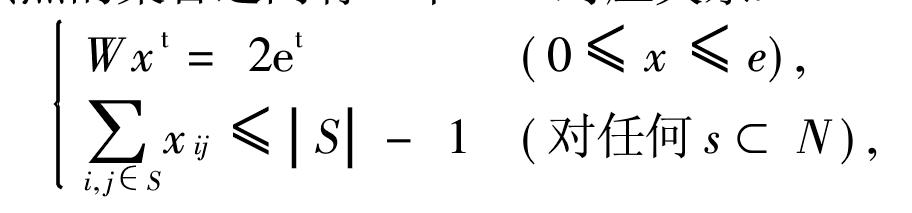
其中,W為Kn關聯矩陣,e=(1,1,…,1)為一個n維向量,x=(x1,x2,…,xε),ε=n(n-1)/2,為ε維向量,t表示向量的轉置。由此,哈密頓多面體就是上面方程和不等式組整數解集的凸包。任何一個哈密頓圈均相應旅行售貨員問題(參見“旅行售貨員問題”)的一個可行解。也可以說,哈密頓多面體為旅行售貨員問題所有可行解的凸包。若將Kn用K*n代替,即將Kn的每一邊用兩個有向邊代替,在K*n上考查有向哈密頓圈,則在K*n上的所有有向哈密頓圈的鄰接矩陣的凸包稱為有向哈密頓多面體。若在旅行售貨員問題中,將可行解限制在有向哈密頓圈上,則這時被稱為有向旅行售貨員問題,或非對稱旅行售貨員問題。相應地,原旅行售貨員問題也稱為對稱旅行售貨員問題。由此,有向哈密頓多面體也可以說是非對稱旅行售貨員問題所有可行解的凸包。
哈密頓圈問題
圖論中著名的難題之一。設有一個圖,若其上存在一個圈,這個圈包含該圖上的每一節點,則稱該圈為哈密頓圈,這個圖稱為哈密頓圖。哈密頓圈問題可敘述為:什麼樣的圖為哈密頓圖,或者說判斷一個圖是哈密頓圖的行之有效的充分必要條件是什麼。目前這一問題尚未解決。關於哈密頓圈的研究,最早是歐拉(Euler,L.)研究騎士(相當於中國象棋中的馬)從棋盤上的某一位置出發,走遍所有可能的位置且每個位置只通過一次後,回到原來的位置。而哈密頓(Hamilton,W.R.)研究環遊世界的遊戲是在歐拉之後近一個世紀,然而卻由此開始引起人們對於這個問題的注意。實際上,哈密頓的遊戲就是,在一個正十二面體上,從一個頂點開始沿著棱走遍所有的十二個頂點回到原地,使得每一頂點只通過一次。就是在十二面體相應的圖上求一個哈密頓圈。若一個圖上存在一條路,這條路包含該圖上的所有節點,則稱該圖為可跡圖,稱這樣的路為哈密頓路。若對於一個圖上的每一節點,存在一個以該節點為始點的哈密頓路,則稱該圖為齊次可跡圖。一個圖被稱為哈密頓連通圖,若對於這圖上任何兩節點,存在一條哈密頓路連結這兩節點。稱一個圖為亞哈密頓圖,若從這圖上去掉無論哪一節點,所得的圖都是哈密頓圖。稱一個圖為亞可跡圖,若從這圖上去掉無論哪一節點,所得的圖都是可跡圖。
哈密頓圖
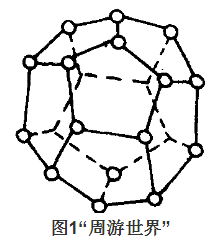
1859年,英國數學家哈密頓提出一種名為“週遊世界”的遊戲。他用正十二面體(如圖1)的20個頂點代表20個大城市,要求沿著棱從一個城市出發,經過每個城市恰好一次,然後回到出發點。
這個遊戲曾經風靡一時。為了清楚起見,我們作一個平面圖(如圖2),與這個十二面體的頂點和棱所組成的圖同構,則圖中粗的邊組成的圈就是一個所求的路線。我們還可以找到其他的路線。
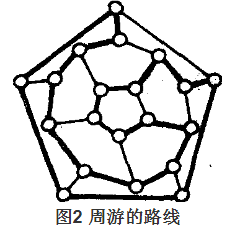
一般地,在一個給定的圖中,若存在一條迴路,經過每個頂點恰好一次,則這個迴路稱為哈密頓迴路;若一個圖中可以找到一個哈密頓迴路,則這個圖稱為哈密頓圖。表面上看哈密頓圖的概念與歐拉圖的概念非常相似,但兩者迥然不同。可以找到一個歐拉圖但不是哈密頓圖的例子,也可以找到一個哈密頓圖但不是歐拉圖的例子。
對哈密頓圖的判定問題,迄今還沒有像歐拉圖那樣能找到一個很漂亮的充分必要條件。奧爾給出了一個很重要的充分條件:G為簡單圖,頂點數n≥3,且對每一對不相鄰的點u,v,有:

哈密頓
英國數學家、物理學家。生於愛爾蘭都柏林(Dublin),卒於都柏林。他自幼才智過人,5歲時能讀拉丁語、希臘語和希伯來語,14歲時已學會12種語言。1823年入都柏林三一學院學習。1827年被聘為該校天文學教授,並獲得皇家天文學家的稱號。1837—1845年任愛爾蘭皇家學院院長,並被選為多個科學院和學術機構的成員。1836年獲倫敦皇家學會皇家勳章。
哈密頓早年曾精讀牛頓(Newton,I.)和拉普拉斯(Laplace,P.-S.)的著作,1822年撰文指出拉普拉斯的《天體力學》中的一個錯誤,從此開始數學研究。他對數學的主要貢獻是創立了四元數理論和發展了變分法和微分方程理論。1835年,撰文詳細討論複數x+iy的性質,進而試圖尋找三維“複數”,由此導致創立了形如a+bi+cj+dk(a,b,c,d為實數)的所謂四元數,這是一種不同於實數系和複數系的新數系。四元數的出現,深化了人們對“數”的認識,推動了向量代數、向量分析和物理學的發展。哈密頓用分析的方法研究幾何光學,引入了特徵函式概念,並利用這一概念和最小作用原理(亦稱哈密頓原理)把光學和動力學的問題轉化為變分法問題。他建立的動力學方程稱為“哈密頓正則方程”,其中以廣義坐標和廣義動量作為獨立變數,代表總能量的函式H稱為“哈密頓函式”。這些結果在現代物理學中獲得廣泛套用。他的主要著作有《四元數講義》(1853)、《光束論》(1827)和《動力學一般方法》(1834)等。
