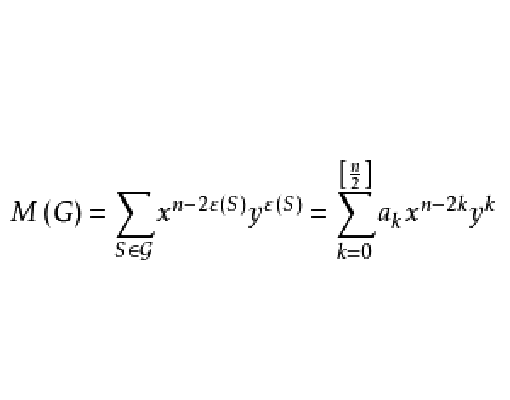匹配多項式(matching polynomial)是圖的一種多項式，設F由G中所有子圖K1及K2所構成，它們的度量分別為x及y，由這種單元組成的點覆蓋S就是圖G的“匹配”(matching)；它對應的單項式為xn-2ε(S)yε(S)，其中ε(S)為S中單元K2的數目(邊數)，這個單項式對應相應的多項式就是圖G的匹配多頂式。。
基本介紹
- 中文名：匹配多項式
- 外文名：matching polynomial
- 所屬學科：數學（圖論）
- 屬性：圖的一種多項式
- 相關概念：匹配，點覆蓋多項式，點覆蓋等
基本介紹,相關定義,邊(點)覆蓋多項式,匹配多項式的定義,相關概念,相關定理,圖論,
基本介紹
相關定義
定義1取定圖G的一個子圖族
；對其中每一個子圖
，賦以某一整環R中之元
，作為它的度量，這樣一個具有度量的子圖族便稱為“覆蓋單元集”；其中每一個子圖α稱為“(覆蓋)單元”。
定義2對於不含全不連通子圖的覆蓋單元集而言，圖G的一個“邊覆蓋”，是指由若干個無公共邊的單元所組成的集合
，使得
定義2’對給定的覆蓋單元集而言，圖G的一個“點覆蓋”，是指由若干個無公共頂點的單元所組成的集合，使得
邊(點)覆蓋多項式
定義3對給定的覆蓋單元集，設圖G所有邊(點)覆蓋所構成的集族為
，對每一覆蓋
，賦以一個單項式
下文始終採取“空和為零，空積為1“的習慣約定，因此，當
時，P(G)=0，當G=
(空圖)時，只有一個覆蓋
；而
，所以
。其次，在邊覆蓋多項式的情況，增減一些孤立頂點時邊覆蓋不變，因而多項式亦不變；故此時不妨假定圖G並無孤立頂點。
匹配多項式的定義
設由G中所有子圖K1及K2所構成，它們的度量分別為x及y，由這種單元組成的點覆蓋S就是圖G的“匹配”(matching)；它對應的單項式為
，其中
為S中單元K2的數目(邊數)，於是
相關概念
1．圈多項式
在無向圖的情況，設由G中所有的K1(一點生成子圖)、K2(一邊生成子圖)及初級圈(點數≥3)所構成，R為實數域上的多項式環，由此產生出的點覆蓋多項式通常稱為“圈多項式”，特別當單元K1的度量為
(未定元)，K2的度量為-1，其它初級圈的度量為-2時，點覆蓋多項式
2.子圖多項式
當G為無向圖，由G的一切連通子圖所構成時，圖G在之下的點覆蓋多項式稱為“子圖多項式”，而當單元
的度量
不同時，可得一些特殊的多項式，例如：
(1°) 對每一單元，賦以度量
，其中
為連通子圖α的圈秩，那么圖G在這種覆蓋意義下的多項式
(2°) 若令
，其中
為連通子圖α的秩，則
(3°) 若令
，其中
為連通子圖α的邊數，則
相關定理
設圖G= (V，E)在單元集之下的邊(點)覆蓋多項式為P(G)，下面將給出這兩類多項式的一般消去定理。
定義4對任意的頂點子集
及邊子集
，二元組
稱為G的“偽子圖”。
當
中每條邊所關聯的頂點均屬於
時，就是通常意義的子圖，
將簡記為
。
定義5給定G的一個偽子圖H，圖G關於H的部分邊(點) 覆蓋SH，是指由若干個無公共邊(點)的單元所組成的集合，這些單元的並包含了H的全部頂點和邊，且每個單元都至少含有H的一個頂點或一條邊。
對於圖G的一個邊(點)覆蓋S 而言，如果S覆蓋著H的點和邊，則將S 中含有H的頂點或邊的單元取出來，這樣構成的子集SH一定是關於H的部分覆蓋，即有
，但反過來說，一個部分覆蓋卻不一定能成為某個覆蓋的子集(它未必能添上一些單元後構成G的覆蓋)。
定義6對部分邊(點)覆蓋
而言，其相應的單項式定義為
特別當
，因而
時，
。
此外，我們記
。
現在，分兩種情況討論。
邊覆蓋多項式的消去定理
定義7一個關於H的部分邊覆蓋SH稱為極大的，如果不存在以它為真子集的另一個關於H的部分邊覆蓋
。
命題 對任一個邊覆蓋
，由其中所有含有H的頂點或邊的單元所構成的部分邊覆蓋SH一定是極大的。
證明：設
是按上述方式導出的部分邊覆蓋，那么H中的邊(
)及H中的頂點所關聯的邊(
的端點
)均被SH的單元所覆蓋；而任一單元均非孤立點，所以不存在這樣的單元，它與SH的單元無公共邊而又包含H的頂點或邊，故SH為極大的。
定理1設圖G在單元集之下的邊覆蓋多項式為P(G)，並設
為G的一個偽子圖，則
點覆蓋多項式的消去定理
取定圖G的一個偽子圖
，考察由它除去一些邊所成的偽子圖H的集合
定理2 設圖G在單元集之下的點覆蓋多項式為P(G)，並設為G的一個偽子圖，則
圖論
圖論(graph theory)是組合學的一個分支，它所研究的是一個集合連同其上的一個二元關係所形成的模型，稱之為圖。歷史上最早以這種抽象的圖的模型研究問題的是歐拉(L.Euler)，他於1736年，以這種抽象的模型解決了哥尼斯堡七橋問題，並且發現了一個圖存在歐拉環遊的條件、此外，歐拉對圖論的貢獻還有：第一次引進了哈密頓圈；注意到多面體的頂點數、棱數和面數之間存在一個簡單的關係，他所解決的騎士在棋盤上的旅行路線問題就是討論哈密頓圈的存在，這些足以使他成為圖論之鼻祖，可惜的是在中國文化發展的浩瀚文獻中除了幾何圖形之外竟至今還沒有發現在20世紀之前有關這種抽象的圖的蛛絲馬跡。
圖論的早期發展多起因於數學遊戲，歐拉之後半個世紀，高斯(C.F.Gauss)提出棋盤上的8後問題，實際上相當在一圖上求一個最大獨立集。他還研究過平面上的閉曲線的相交問題。第一次引出一個序列的交圖並且提出僅用交圖之結構性質即可確定一個序列是否對應於一個平面閉曲線交點形成的序列的一個猜想。19世紀中葉，在利斯廷(J.B.Listing)的文章中出現了迷宮的遊戲.其後，塔里(G.Tarry)所提供的方法實際上就是人們今天所說的深探法和追蹤法.英國數學家柯克曼(T.P.Kirkman)以他解決的15女生問題而著稱，實際上，這個問題可以轉化為確定一個圖的色數的問題，1852年，格思里(F.Guthrie)提出四色問題，40年後，希伍德(P.J.Heawood)又提出一般的地圖著色問題，1880年泰特(P.G.Tait)就注意到了3正則圖的1因子分解，1891年，佩特森(J.Petersen)證明了3正則圖存在一個1因子，從而，真正開始了圖的對集、因子以及因子分解的理性發展，直到1947年，塔特(W.T.Tutte)才建立了圖的因子分解理論的成熟基礎。
另一方面，從19世紀中葉起，首先是德國物理學家基爾霍夫(G.R.Kirchhoff)從電網路的研究中發現圖中的圈可以用基本圈表示，並且得到了基本圈的數目與圖的節點數和邊數的線性關係，接著，凱萊(A.Cayley)第一次使引進樹，並且研究了各種樹的計數，他在這方面的工作一直影響到1935年波利亞(G.Polya)關於一般圖的計數理論的建立，可惜的是，凱萊關於樹的計數的成果開始並未在他的故鄉英國引起注意，卻很快在德國產生了影響，由於那時布朗(A.C.Brown)引進了原子的圖形表示，所以這就使得樹的計數可以直接套用到確定同分異構的碳水化合物的工作，這就是化學中套用圖論的開端，1878年，西爾維斯特(J.J.Sylvester，)在他的學術文章中第一次用現代意義下“圖”這個術語。
20世紀初，開始跨入平面圖的理論，雖然，若爾當(M.E.C.Jordan)首先意識到平面上不自交的閉曲線將平面分劃為內、外部兩個區域，但是，直到1905年，才由維布倫(O.Veblen)給出第一個正確的證明，20世紀30年代初，庫拉托夫斯基(K.Kuratowski)發表了第一篇判定一個圖是否為可平面圖的文章，其後不久，惠特尼(H.Whitney)的一系列有關圖論的理論結果大部分是對於可平面圖的，特別是他提出代數對偶的概念解決了判定圖的平面性問題.接著，麥克萊恩(S.MacLane)、吳文俊、塔特等都曾相繼在這方面建立了他們各自的理論。在20世紀初，伯克霍夫(G.D.Birkhoff)第一次引進圖的色多項式的概念並對此做了系統的研究，開闢了圖論中一個重要新課題.近半個世紀之後，塔特發展到范色多項式並且揭示了它與圖的內在結構性質的關係，而這種關係在其後20餘年瓊斯(V.F.R.Jones)發現的在3維空間中扭結的新的拓撲不變數——瓊斯多項式中竟得到再現。
然而，不管怎樣，塔特等人於1940年所發表的關於拼方的文章，創立了電網路上的一種數學理論，解決了純數學的一個難題，打開了現代圖論研究的序幕，這篇文章不僅解決了拚方的問題，而且引出了一系列重要的圖論問題，例如，圖的連通性、定向、對稱性以及還用到了平面性與對偶性等，這些至今在圖論的研究中仍很活躍。尤其是他們所揭示的方法還深刻地影響到網路流的理論、曲面嵌入的理論，並促進了集以及因子分解的理論、著色理論，以至擬陣論與組合幾何的形成與發展。
圖論在近半個世紀以來的發展是空前的.除上面提及的一些重要方面外，還出現了極圖理論、隨機圖論、代數圖論、拓撲圖論等新的分支。同時，也出現了各種統一性的理論研究，如超圖、擬陣以至於組合幾何，其發展更是日新月異，圖論還廣泛而且愈來愈深入地滲透和套用到其他科學中去，除原來在物理學和化學中的套用又得到廣泛和深入的發展之外，還深入到了生物學和生物工程以及經濟和社會科學的各領域.尤其值得注意的是，隨著電子技術和現代計算機的發展，提出了層出不窮的新的數學問題，其中，很多問題與圖論有密切的關係，對於它們的深入研究將會形成新的理論分支。例如，算法及其複雜性的理論和組合計算幾何的出現與發展等，就是直接的產物.在圖論近50年來的成果中，四色問題的計算機驗證、希伍德地圖著色問題的解決以及塔特多項式的出現等，也是對整個數學領域的重要貢獻。
關於中國在圖論方面近30年來的發展，可參見顏基義等人在《中國自然科學年鑑》1989年卷的數學進展專欄中發表的文章。
