傅立葉積分運算元(Fourier integral operator)是偏微分運算元理論中的重要工具。它和擬微分運算元一起,被稱為“70年代技術”。擬微分運算元的前身是具強奇性的卷積型奇異積分運算元。
基本介紹
- 中文名:傅立葉積分運算元
- 外文名:Fourier integral operator
- 類別:相關辭彙
- 闡述:偏微分運算元理論中的重要工具
- 相關:奇異積分運算元
- 套用學科:數學術語
概述
基本原理
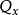

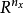
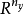
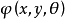



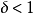
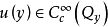
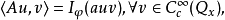
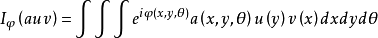
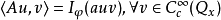
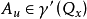
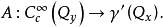
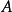
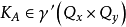
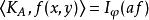
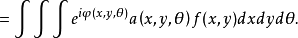

傅立葉積分運算元(Fourier integral operator)是偏微分運算元理論中的重要工具。它和擬微分運算元一起,被稱為“70年代技術”。擬微分運算元的前身是具強奇性的卷積型奇異積分運算元。
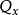

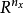
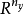
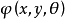



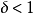
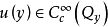
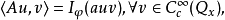
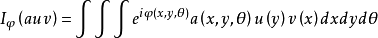
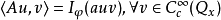
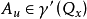
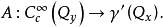
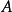
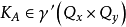
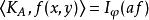
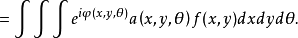
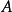
傅立葉積分運算元(Fourier integral operator)是偏微分運算元理論中的重要工具。它和擬微分運算元一起,被稱為“70年代技術”。擬微分運算元的前身是具強奇性的卷積型奇異...
仿傅立葉積分運算元是現代微分運算元理論中的一種重要的運算元。F(p)在仿微分運算元理論中有許多與傅立葉積分運算元在擬微分運算元理論中相似的性質。...
傅立葉積分運算元理論及其套用是由科學出版社出版的書籍,作者是仇慶久陳恕行是嘉鴻劉景麟蔣魯敏,在1997年出版。...
等人推廣了奇異積分運算元理論,創建了擬微分運算元理論。繼而,又出現了傅立葉積分運算元理論。它們結合微局部分析方法,線上性微分方程理論的研究中發揮了“革命”性的作用...
,故柯西奇異積分運算元是二次代數運算元,又如,希爾伯特空間的投影運算元 P,滿足方程 ,但 ,故它是二次代數運算元。再如,傅立葉積分運算元滿足方程 ,但不滿足低於四次的方...
在時頻平面上若將Fourier變換看作從時間軸逆時針旋轉90度到頻率軸,則分數階Fourier變換運算元就是可旋轉任意角度的運算元,故可認為分數階Fourier變換是一種廣義的Fourier...
“文化大革命”一結束,王柔懷立即恢復了關於基本理論的研究,並把主要注意力轉向當時在國際上蓬勃發展的一般偏微分運算元理論,包括擬微分運算元,傅立葉積分運算元和馬斯洛夫...
微局部分析是偏微分方程運算元理論中的一個重要的研究領域。在擬微分運算元及傅立葉積分運算元理論中,常將所論問題化為對相應的象徵(及位相)的處理。實際上,現代微分...
近二三十年進展較快,且在當前國際上有較多人研究的偏微分方程問題有:線上性問題方面,微分運算元的概念已先後推廣為擬微分運算元、傅立葉積分運算元和仿微分運算元,利用...
1995.05 《擬微分運算元 第2版》 陳恕行編著 北京:高等教育出版社 1997 《現代數學基礎叢書 傅立葉積分運算元理論及其套用》 仇慶久,陳恕行,等 北京:科學出版社 1998...
合著有《傅立葉積分運算元理論及其應 用》、《仿微分運算元引論》及論文20多篇。詞條標籤: 人物 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 最近...
它將波動光學和幾何光學聯繫起來,並為傅立葉積分運算元提供了一個雛型。 [1] 特徵超曲面雙曲型微分方程 編輯 雙曲型偏微分方程是描述振動或波動現象的一類重要的...
微分方程的一般理論、廣義函式與Sobolev空間、橢圓邊值問題、能量方法、運算元半群...出版專著有:《傅立葉積分運算元理論及其套用》、《仿微分運算元引論》發表論文七十...
16.3 有界積分運算元的例子16.4 雙曲方程的解運算元16.5 熱傳導方程的解運算元16.6 奇異積分運算元,擬微分運算元和Fourier積分運算元第17章 Banach代數及其基本譜理論...
