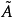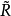代數集是特殊的集合,它是若干個多項式的公共根的集合,是與代數簇密切相關的概念。
基本介紹
- 中文名:代數集
- 外文名:algebraic set
- 所屬學科:數學
定義,性質,代數簇,
定義
代數集是特殊的集合,它是若干個多項式的公共根的集合,是與代數簇密切相關的概念。設 S 是域 K 上多項式環 的若干個多項式的集合,記
的若干個多項式的集合,記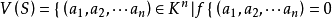 ,對任意
,對任意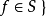 為 S 中所有多項式的公共根的集合,對於 Kn 中的子集 T,若存在集合
為 S 中所有多項式的公共根的集合,對於 Kn 中的子集 T,若存在集合 使得 T=V(S),則稱 T 為一個代數集,故 V(S)=V((S))。因此,K中每個代數集皆為 V(ℜ) 的形式,其中
使得 T=V(S),則稱 T 為一個代數集,故 V(S)=V((S))。因此,K中每個代數集皆為 V(ℜ) 的形式,其中

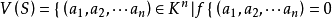
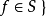

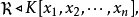
性質
代數集的交與空集合 以及 Kn=V(0) 皆為代數集。反之,設 A 是Kn的一個子集合,若
以及 Kn=V(0) 皆為代數集。反之,設 A 是Kn的一個子集合,若


則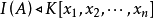 稱為集合 A 對應的多項式理想。
稱為集合 A 對應的多項式理想。
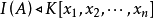
另一方面,當 K 為代數閉域時,Kn 中代數集的全體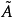 與
與 中根理想的全體
中根理想的全體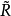 在映射
在映射 下
下 是反序一一對應的。
是反序一一對應的。