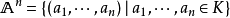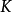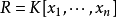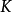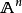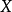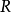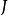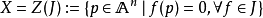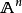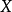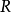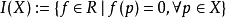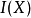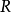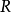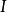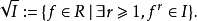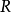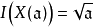希爾伯特零點定理

希爾伯特零點定理（Hilbert's Nullstellensatz）是古典代數幾何的基石, 它給出了域 k 上的 n 維仿射空間中的代數集與域 k 上的 n 元多項式環的根理想的一一對應關係, 此外, 它的一個較弱版本給出了仿射空間中的點與多項式環的極大理想之間的一一對應關係, 由此建立了代數和幾何之間的聯繫, 使得人們可以用交換代數的手段研究幾何問題.

基本介紹

• 中文名：希爾伯特零點定理
• 外文名：Hilbert's Nullstellensatz
• 套用：是解方程的基礎定理之一
• 可計算性：可以用於具體判斷方程組是否有解
• 諾特定理：由希爾伯特零點定理推出
• 涉及學科：數學, 交換代數, 代數幾何

各種形式

初等形式

設是關於變元 一組 元多項式. 方程組無公共零點的充要條件是: 存在另一組元多項式,使得成立: .

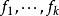
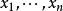
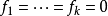
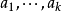
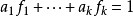
弱形式

代數閉域 上的 元多項式環的極大理想具有形式, 這裡.

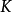
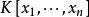
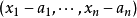
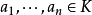
強形式

強形式的表述需要定義代數集. 稱集合 是代數閉域上的維仿射空間, 又記 為上的元多項式環. 稱 的子集 為代數集, 如果存在 的理想 使得. 另一方面, 對於的任一子集, 我們都可以定義的一個理想, 不難驗證是的一個根理想. 這裡,的理想的根理想定義為

希爾伯特零點定理的強形式現在可以表述如下:的任一理想都滿足.