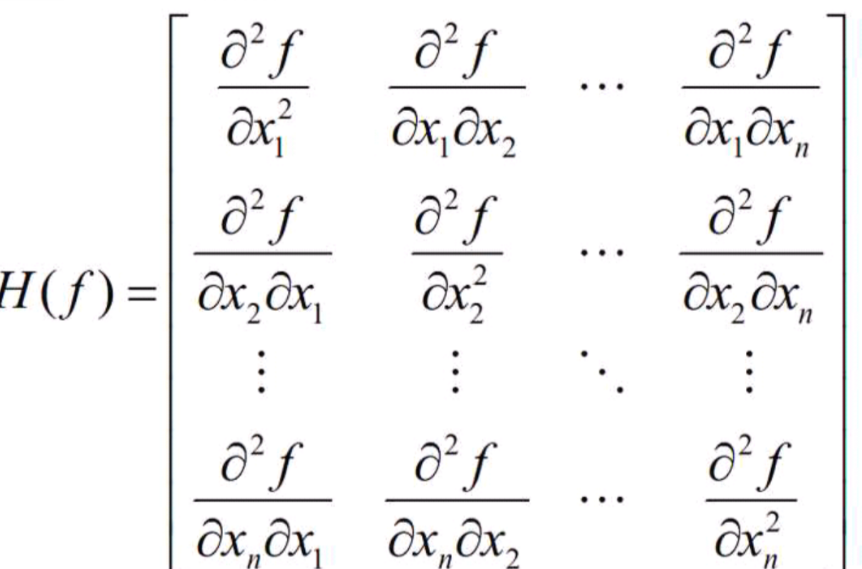基本介紹
- 中文名:黑塞矩陣
- 外文名:Hessian Matrix
- 別名:海森矩陣,二階導數矩陣
- 提出時間:19世紀
- 提出者:德國數學家Ludwig Otto Hesse
- 特點:黑塞矩陣為對稱陣
- 套用學科:線性代數、運籌學
定義,二元函式的黑塞矩陣,多元函式的黑塞矩陣,對稱性,利用黑塞矩陣判定多元函式的極值,定理,實例,
定義
在工程實際問題的最佳化設計中,所列的目標函式往往很複雜,為了使問題簡化,常常將目標函式在某點鄰域展開成泰勒多項式來逼近原函式。
二元函式的黑塞矩陣


其中, 。
。

將上述展開式寫成矩陣形式,則有:

即:

其中:

多元函式的黑塞矩陣

其中:
(1) ,它是
,它是 在
在 點處的梯度。
點處的梯度。



(2) 為函式
為函式 在
在 點處的黑塞矩陣。
點處的黑塞矩陣。



對稱性
原因:如果函式 的二階偏導數連續,則二階偏導數的求導順序沒有區別,即
的二階偏導數連續,則二階偏導數的求導順序沒有區別,即





利用黑塞矩陣判定多元函式的極值
定理
設n多元實函式 在點
在點 的鄰域內有二階連續偏導,若有:
的鄰域內有二階連續偏導,若有:



並且

則有如下結果:
(3)當A不定矩陣時, 不是極值點。
不是極值點。

實例
求三元函式 的極值。
的極值。

解:因為 ,故該三元函式的駐點是
,故該三元函式的駐點是 。
。


又因為 ,
,

故有:

因為A是正定矩陣,故 是極小值點,且極小值
是極小值點,且極小值 。
。