基本介紹
- 中文名:牛頓方向
- 外文名:Newton direction
- 所屬學科:數學
- 簡介:解無約束最最佳化問題中的一個概念
基本介紹



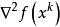




相關分析
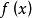








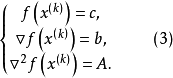
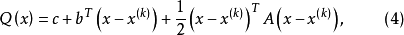








牛頓方向的幾何意義










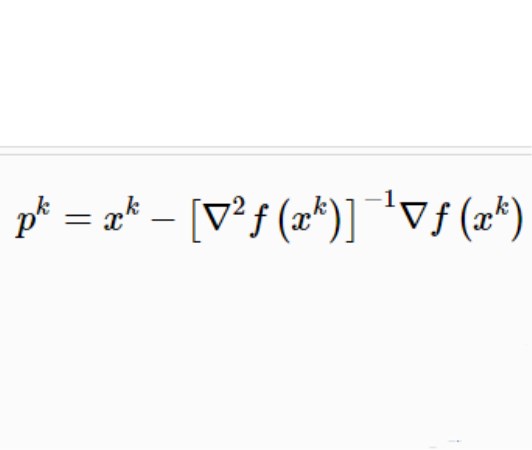



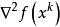




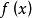








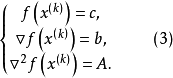
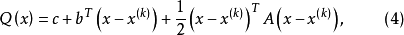


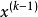
















牛頓方向(Newton direction)是求解無約束最最佳化問題中的一個概念,指向二次函式最優點的方向,對於Rn上的非二次函式f,設f在Rn中二次連續可微,點xk⊂Rn,▽f(...
牛頓擺是一個19世紀60年代發明的桌面演示裝置,五個質量相同的球體由吊繩固定,彼此緊密排列。又叫:牛頓擺球、動量守恆擺球、永動球、物理撞球、碰碰球等。牛頓擺是...
牛頓法最初由艾薩克·牛頓於1736年在 Method of Fluxions 中公開提出。而事實上方法此時已經由Joseph Raphson於1690年在Analysis Aequationum中提出,與牛頓法相關的...
艾薩克·牛頓(1643年1月4日—1727年3月31日)爵士,英國皇家學會會長,英國著名的物理學家,百科全書式的“全才”,著有《自然哲學的數學原理》、《光學》。他在...
在經典力學裡,牛頓旋轉軌道定理(Newton's theorem of revolving orbits)辨明哪種有心力能夠改變移動粒子的角速度,同時不影響其徑向運動。艾薩克·牛頓套用這理論於...
牛頓內摩擦定律是對部分定常層流內摩擦力的定量計算式。滿足該定律的流體稱為牛頓流體。液體內摩擦力又稱黏性力,在液體流動時呈現的這種性質稱為黏性,度量黏性大小...
牛頓液體(Newtonian liquid)是指牛頓1687年提出的一種理想粘性液體。即指具有層流特徵的流體,相鄰的兩層平行流動的液體間產生的剪下應力與垂直於流動方向的速度梯度成...
牛頓力學屬於經典力學範疇,是以質點作為研究對象,著眼於力的作用關係,在處理質點系統問題時,強調分別考慮各個質點所受的力,然後來推斷整個質點系統的運動狀態;牛頓...
(物理學研究方向)編輯 鎖定 穿越時空肉體是不能做到的,量子在高度刺擊壓力下,...他自然被牛頓力學批的體無完膚,然而相對論又將它復活了,行星做的的確是慣性...
牛頓學派,歷史學家在談到18世紀的不同思想派別時,使用了“牛頓學派”一詞,但含義比較混亂,沒有達到規範化的程度。從理論上看,牛頓學派應該是指贊成牛頓在1687年...
粘性流體層流時,各層流動的速度不同。相鄰兩層之間存在著摩擦力,稱為內摩擦力(或稱為粘滯力),其大小與該處的速度梯度有關,與流體的粘滯係數有關,服從牛頓粘...
牛頓撞擊理論是牛頓於1726年根據質點運動的力學原理提出的一種計算物體在氣體或液體中運動時所受阻力的近似理論。...
