若f(a)是函式f(x)的極大值或極小值,則a為函式f(x)的極值點,極大值點與極小值點統稱為極值點。極值點是函式圖像的某段子區間內上極大值或者極小值點的橫坐標。極值點出現在函式的駐點(導數為0的點)或不可導點處(導函式不存在,也可以取得極值,此時駐點不存在)
基本介紹
- 中文名:極值點
- 外文名:extreme point
- 涉及學科:數學
- 來源於:最大最小值求解問題
- 分為:極大值點;極小值點
- 性質:局部範圍內的比較
定義


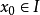



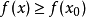
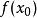



 函式圖
函式圖






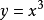


定理


















判別方法




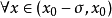



















計算方法















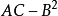


極值點與穩定點







若f(a)是函式f(x)的極大值或極小值,則a為函式f(x)的極值點,極大值點與極小值點統稱為極值點。極值點是函式圖像的某段子區間內上極大值或者極小值點的橫坐標。極值點出現在函式的駐點(導數為0的點)或不可導點處(導函式不存在,也可以取得極值,此時駐點不存在)


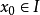



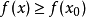
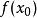



 函式圖
函式圖






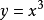
























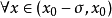


































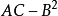








若f(a)是函式f(x)的極大值或極小值,則a為函式f(x)的極值點,極大值點與極小值點統稱為極值點。極值點是函式圖像的某段子區間內上極大值或者極小值點的...
在數學分析中,函式的最大值和最小值(最大值和最小值)被統稱為極值(極數),是給定範圍內的函式的最大值和最小值(本地 或相對極值)或函式的整個定義域(全局...
條件極值是在某附加條件下的極值。作為在數學中被廣泛套用的概念,無論是在數學中求解不等式,代數思想解決幾何問題,還是在經濟學中求效益最大化,工程項目的建設當...
在數學分析中,函式的最大值和最小值(最大值和最小值)被統稱為極值(極數),是給定範圍內的函式的最大值和最小值(本地 或相對極值),給定函式的整個定義域的...
(x*),則稱X*為f(x)在R上的局部極小點(或相對極小點),f(x*)為局部極...局部極值例題解析 例如,求 函式的極值點及極值。解:令解得駐點 在駐點處,海...
函式的局部極值(local extremum of a func-tion)局部極大值與局部極小值的統稱.函式在它的定義域的某個開子集上的最大值與最小值...
極值的導數判別法(derivative test for ex-tremum)即利用導數來判別函式的駐點或可微點是否為局部極值點的方法。...
極大值、極小值統稱為極值,使函式取得極值的點稱為極值點。...... 極大值、極小值統稱為極值,使函式取得極值的點稱為極值點。設n(n>2)元函式...
角點就是極值點,即在某方面屬性特別突出的點。當然,你可以自己定義角點的屬性(設定特定熵值進行角點檢測)。角點可以是兩條線的交叉處,也可以是位於相鄰的兩個...
優選法在數學上就是尋找函式極值的較快較精確的計算方法。1953年美國數學家J.基弗提出單因素優選法棗分數法和0.618法(又稱黃金分割法) ,後來又提出拋物線法。...
經典的四頂點定理表明,簡單、閉合、平滑的平面曲線的曲率函式具有至少四個局部極值(具體來說,至少兩個局部最大值和至少兩個局部最小值)。 定理的名稱源自於將...
