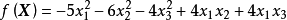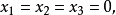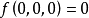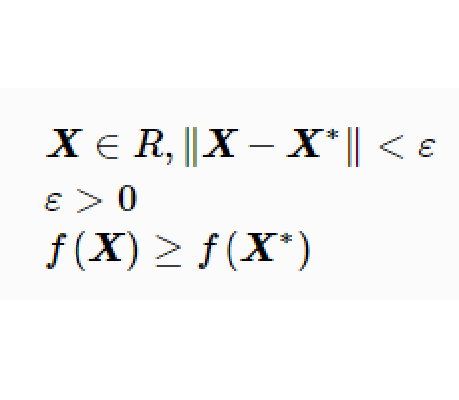設f(x)為定義在n維歐式空間En的某一個區域R上的n元實函式,其中X=(x1,x2,…,xn)T。
對於X*∈R,如果存在某個ε>0,使所有X*的距離小於ε的X∈R(即X∈R且||X-X*||<ε)均滿足不等式f(x)≥f(x*),則稱X*為f(x)在R上的局部極小點(或相對極小點),f(x*)為局部極小值。若對於所有X≠X*且與X*的距離小於ε的X∈R,f(x)>f(x*),則稱X*為f(x)在R上的嚴格局部極小點,f(x*)為嚴格局部極小值。
如將上述不等式反向,即可得到相應的極大點和極大值的定義。
基本介紹
- 中文名:局部極值
- 外文名:local extremum
- 所屬學科:數理科學
- 別名:相對極小點
局部極值的定義



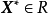



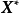

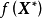

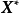


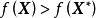
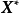

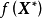


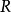
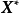


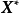


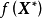



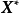

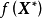
極值存在的條件
極值存在的必要條件

極值存在的充分條件
例題解析