使泛函達到極值的變元函式稱為極值函式,若它為一元函式,通常稱為極值曲線。極值也稱為相對極值或局部極值。
基本介紹
- 中文名:極值曲線
- 外文名:extremum curve
- 適用範圍:數理科學
簡介
歐拉方程的積分曲線

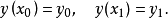


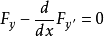

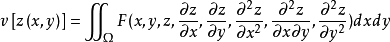
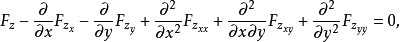
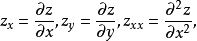
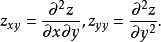
局部極值



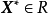



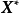

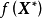

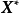


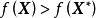
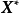

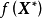






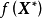



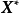

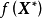

使泛函達到極值的變元函式稱為極值函式,若它為一元函式,通常稱為極值曲線。極值也稱為相對極值或局部極值。

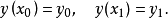


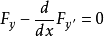

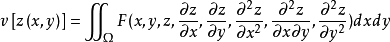
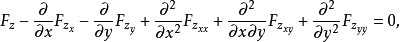
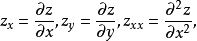
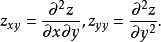








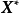


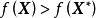
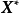

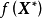


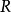
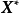


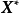


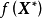



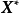

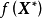
使泛函達到極值的變元函式稱為極值函式,若它為一元函式,通常稱為極值曲線。極值也稱為相對極值或局部極值。...
在數學分析中,函式的最大值和最小值(最大值和最小值)被統稱為極值(極數),是給定範圍內的函式的最大值和最小值(本地 或相對極值)或函式的整個定義域(全局...
使泛函達到極值的變元函式稱為極值函式,若它為一元函式,通常稱為極值曲線。...... 使泛函達到極值的變元函式稱為極值函式,若它為一元函式,通常稱為極值曲線。...
在數學分析中,函式的最大值和最小值(最大值和最小值)被統稱為極值(極數),是給定範圍內的函式的最大值和最小值(本地 或相對極值),給定函式的整個定義域的...
曲線,是微分幾何學研究的主要對象之一。直觀上,曲線可看成空間質點運動的軌跡。微分幾何就是利用微積分來研究幾何的學科。為了能夠套用微積分的知識,我們不能考慮...
在工程設計或科學實驗中所得到的數據往往是一張關於離散數據點的表 ,沒有解析式來描述 x-y關係。根據所給定的這些離散數據點繪製的曲線,稱為不規則曲線,通常用...
理論頻率曲線是為了綜合反映水文變數的地區規律性,克服經驗頻率曲線外延的主觀性,水文頻率計算引入了能用數學方程式表示的頻率曲線來配合經驗頻率曲線點距。...
在計算機視覺領域,最大穩定極值區域 (MSER)(Maximally Stable Extremal Regions)是一種用於在圖像中進行斑點檢測的方法。這個方法由Matas等人提出,用於在兩個不同視角...
水文要素值與其發生頻率之間的關係曲線,它是推求工程水文設計值的重要工具。...... 有的國家也用對數正態曲線或極值I型曲線。水文頻率曲線參數估計 一般頻率曲線所含...
平穩曲線場(field of stationary curve)為研究強極值充分條件而引進的平穩曲線簇.設S。是三維歐氏空間中的某個曲面,利用橫截條件,從S。中的每一點M都可作出泛函...
測井曲線特徵是指在測井時形成的曲線反應出不同岩性、層位特徵,進而根據所得曲線判斷出具體岩性、層位等。...
明渠水流自由水面的縱剖面線。由於明渠均勻流的水面曲線是平行於渠底的直線,比較簡單,因此明渠水面曲線主要研究的是非均勻流。分析與計算水面曲線是作好明渠設計與有...
短程線問題(shortest distance problem)亦稱“測地線問題”,是變分學中的一個重要問題。設A、B為某一曲面上二點,求在該曲面上連結A、B且長度取極值的曲線的...
使僅受重力作用且初速度為零的質點從A點到B點沿這條曲線運動時所需時間最短...對泛函求極值的問題稱為變分問題,使泛函取極值的函式稱為變分問題的解,也稱...
