基本介紹
- 中文名:短程線問題
- 外文名:shortest distance problem
- 別稱:測地線問題
- 所屬學科:數學
- 屬性:變分學中的一個重要問題
- 提出者:1697年約翰·伯努利提出
- 相關概念:變分問題,條件極值問題等
基本介紹
變分問題
短程線問題
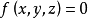

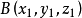
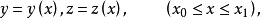


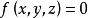
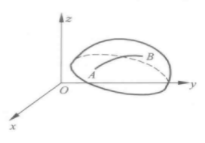 圖1 短程線問題
圖1 短程線問題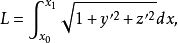
短程線問題的求法
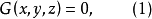

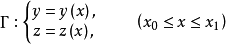
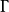
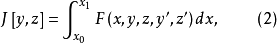
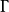
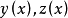
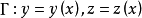
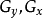
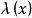
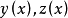


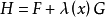
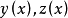
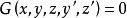
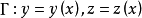
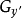

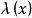
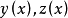
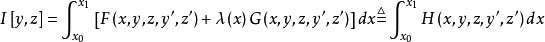
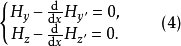
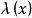
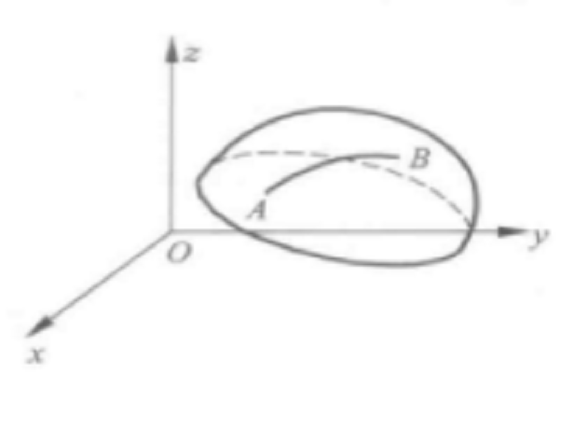
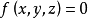

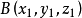
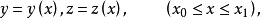


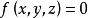
 圖1 短程線問題
圖1 短程線問題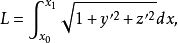
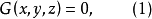

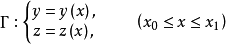
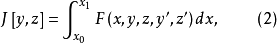
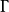
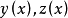
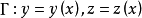
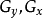
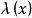
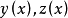


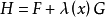
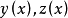
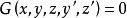
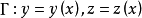
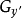

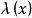
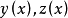
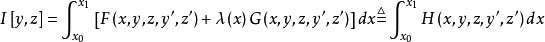
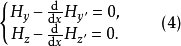
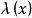
短程線問題(shortest distance problem)亦稱“測地線問題”,是變分學中的一個重要問題。設A、B為某一曲面上二點,求在該曲面上連結A、B且長度取極值的曲線的...
變分問題(variational problem)是有關求泛函的極大值和極小值的問題。最早研究的重要變分問題有:1.最速降線問題:給定不在同一鉛垂線上的兩點A和B,求出連結A...
2、短程線問題:求曲面φ(x,y,z)=0上所給二點間長度最短的曲線,這條最短曲線稱為短程線或測地線。3、基本的等周問題:求長為一定的封閉曲線l,使其所圍的...
2、短程線問題:求曲面φ(x,y,z)=0上所給二點間長度最短的曲線,這條最短曲線稱為短程線或測地線。3、基本的等周問題:求長為一定的封閉曲線l,使其所圍的...
2、短程線問題:求曲面φ(x,y,z)=0上所給二點間長度最短的曲線,這條最短曲線稱為短程線或測地線。3、基本的等周問題:求長為一定的封閉曲線l,使其所圍的...
及端點的條件後,求泛函v的極值問題,稱為條件極 值變分問題或者簡稱條件極值問題.例如,短程線問 題、等周問題以及連續動態系統的最優控制等都是 條件極值問題.[...
最小曲面問題是一個古典變分問題,最小曲面問題的物理背景是空間封閉線框架上的肥皂泡膜問題。在給定的空間封閉線框架上的肥皂泡膜,其具有表面積最小的特性。最小...
正定運算元(positive definite operator)相應運算元方程可以化為變分問題的一類重要運算元...這條最短曲線稱為短程線或測地線。3.基本的等周問題:求長為一定的封閉曲線l...
特雷夫茨法(Trefftz method)是變分問題的一種直接解法,是由特雷弗茨(Trefftz,E...2、短程線問題:求曲面φ(x,y,z)=0上所給二點間長度最短的曲線,這條最短...
若變分問題中待求函式或它們的導數服從某個不等式,這個變分問題的極值就稱為...2、短程線問題:求曲面φ(x,y,z)=0上所給二點間長度最短的曲線,這條最短...
1862年以有關迴轉橢球體(Spheroid)短程線問題的論文獲布雷斯勞大學獎金,同年赴格廷根向黎曼(Riemann, Georg Friedrich Bernhard,1826.17-1866.7.20)求教函式論方面...
橫截條件(transversal condition)是可動邊界的變分問題在端點上滿足的條件。具體...這條最短曲線稱為短程線或測地線。3.基本的等周問題:求長為一定的封閉曲線l...
2、短程線問題:求曲面φ(x,y,z)=0上所給二點間長度最短的曲線,這條最短曲線稱為短程線或測地線。3、基本的等周問題:求長為一定的封閉曲線l,使其所圍的...
變分學的研究對象 17世紀末提出來的最速降線問題、短程線問題和等周問題是歷史上著名的三大變分問題。泛函的極值是變分學的研究對象,其奠基人是L.歐拉、J.-L...
