線性變分問題(linear variational problem)是一類變分問題,指歐拉-拉格朗日方程是線性方程的一類變分問題。
基本介紹
- 中文名:線性變分問題
- 外文名:linear variational problem
- 適用範圍:數理科學
簡介
具體內容
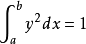
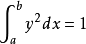
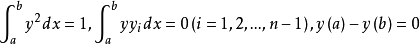
線性變分問題(linear variational problem)是一類變分問題,指歐拉-拉格朗日方程是線性方程的一類變分問題。
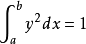
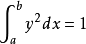
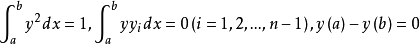
線性變分問題(linear variational problem)是一類變分問題,指歐拉-拉格朗日方程是線性方程的一類變分問題。...
最最佳化理論部分包括最優性理論(含有Lipschitz函式最佳化的Clarke乘子原則以及均衡約束數學規劃問題的最優性條件)、非線性規劃的擾動分析、二階錐的變分分析與二階錐...
變分方法(variational method)是以變分學 和變分原理為基礎的一種近似計算方法,是解決力學和其他領域問題的有效數學工具。...
變分形式(variational formulation)數學物理問題的一種數學表達形式...... ·,·)是定義在VXV上的連續雙線性泛函,且是強制的,.fEV'(V的對偶空間),則變分問題可...
變分一詞用於所有極值泛函問題。微分幾何中的測地線的研究是很顯然的變分性質的...任一個波函式φ都可以展開為哈密頓算符的實際本徵函式的線性組合(我們假定這些...
作為幾何變分問題的解,調和映射的穩定性研究十分重要.若一個調和映射的第二變...近40年來,調和映射理論得到了蓬勃的發展,它與復幾何、代數幾何、非線性分析和...
本書對一般力學、線性彈性靜力學與動力學、線性電磁場理論及壓電材料力學的變分...3.5 彈性動力學初值問題的基本方程3.6 卷積型勢能原理3.7 卷積型余能原理...
線性調節器問題可用變分法、極大值原理或動態規劃來求解。線性調節器分類 編輯 線性調節器可以分為有限時間調節器和無限時間調節器兩類。...
圖像修補等問題中的套用,精選了國內外有關科技文獻的內容,也反映了作者自己的...《圖像處理的變分和偏微分方程方法》由淺入深,首先給出線性模型,然後逐步發展...
結構動力學問題和穩定性問題的有限元方法同時在第12 章介紹了基於其他變分原理...4.4大型線性方程組的求解 67第5 章桿繫結構有限元 715.1桿單元 71...
19.正則變分問題的解是否一定解析;正則變分問題的解是否一定解析1904年,С.Η.伯恩斯坦證明了一個變元的解析非線性橢圓方程其解必定解析。該結果後又被推廣到多...
5.7 非線性泛函分析介紹 /360參考文獻 /369第六章 變分問題及其算法/3716.1 正運算元與二次泛函的極小問題 /3716.2 運算元形式的Euler定理、互補變分原理及變...
在非線性問題方面,研究得較多的有擬線性與完全非線性橢圓及拋物方程、非線性雙...研究中,不動點理論、拓撲度、變分方法(包括臨界點理論)、上(下)解方法、單調...
