橫截條件(transversal condition)是可動邊界的變分問題在端點上滿足的條件。具體形式根據函式形式不同有兩種。
基本介紹
- 中文名:橫截條件
- 外文名:transversal condition
- 領域:數學
- 學科:變分法
- 性質:可動邊界的變分問題
- 形式:2種
概念,變分問題,變分法,
概念
橫截條件(transversal condition)是可動邊界的變分問題在端點上滿足的條件。假設泛函形如:

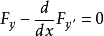
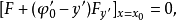

這個條件稱為橫截條件。
2.若A(x0,y0),B(x1,y1)兩端點所在的曲線分別以隱函式形式φ0(x,y)=0,φ1(x,y)=0給出, 其中φ0,φ1有連續偏導數,且:
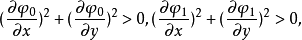
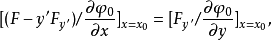
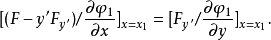
變分問題
有關求泛函的極大值和極小值的問題。最早研究的重要變分問題有:
1.最速降線問題:給定不在同一鉛垂線上的兩點A和B,求出連結A和B的一條曲線使其具有這樣的性質:當質點受重力作用沿著這條曲線由A下滑至B時所需時間為最少。
2.短程線問題:求曲面φ(x,y,z)=0上所給二點間長度最短的曲線。這條最短曲線稱為短程線或測地線。
3.基本的等周問題:求長為一定的封閉曲線l,使其所圍的面積S為極大。
變分法
亦稱變分學,研究泛函極值的一門學科。變分法主要研究泛函的變元函式使泛函達到極值的必要條件和充分條件,並研究求得該變元函式的方法及其性質。變分法的研究方法有直接法與間接法。直接法是直接由泛函去求得極值或判斷相應極值問題是否有解;而間接法是先給出泛函達到極值的必要條件:歐拉-拉格朗日方程(亦稱為歐拉方程),然後在滿足歐拉-拉格朗日方程的解中,利用各種充分條件來判斷變分問題是否有解。
變分法的歷史可追溯到古希臘,那時就有了所謂等周問題:在長度一定的封閉曲線中,找出圍出最大面積的一條封閉曲線。另一著名的問題即最速落徑問題是由伽利略(Galilei,G.)首先提出的.但對變分法實質性研究還是從1696年,約翰第一·伯努利(Bernoulli,Johann Ⅰ)公開向歐洲數學家給出該問題的解開始,洛必達(L'Hospital,G.-F.-A.de)、雅可比(Jacobi,C.G.J.)、約翰第一·伯努利、萊布尼茨(Leibniz,G.W.)、牛頓(Newton,I.)用了不同的方法解決了這個問題。後來歐拉(Euler,L.)和拉格朗日(Lagrange,J.-L.)對這一類問題的研究奠定了變分法的理論基礎.變分法這一名詞由拉格朗日首次提出來,一直沿用下來。
人們研究變分法,是因為社會和自然諸多領域都存在變分原理的實際背景。社會追求效益,投入一定時,希望產出最大;或產出一定時,希望投入最小.某些現象中,自然也依最簡單最有效的方式運行。牛頓在《自然哲學的數學原理》中寫到:“自然不做任何徒勞無益的事情,浪費愈多,服務愈少.自然喜歡簡單性而不為浮華所動”。現代科學早期就依最優原理表達某些自然規律。這一原理看來在一定程度上反映了宇宙的先驗的和諧性,特別吸引那些為知識的統一性和簡單性而奮鬥的科學家。事實上,確實有許多自然規律可用極值原理來表達。第一個發現這種類型的原理是公元前100年,亞歷山大的海倫(Heron,(A))提出的,他用光總走最短路徑解釋光的反射定律.1662年,費馬(Fermat,P.de)從光總是依最快的路徑從一點傳播到另一點這一假設推導出光折射定律。這一假設稱為費馬原理。大約80年後,莫佩蒂(Maupertuis,P.-L.M.de,普魯士科學院院長)斷言,如果自然發生了什麼變化,那么對這一變化所付出的作用量必然是最小的。萊布尼茨對作用引進量綱是“能量×時間”,按照普朗克(Planck,M.)的量子原理(1900年),這個量是基本量子h的整數倍。在莫佩蒂的著述中,作用原理含糊不清,不十分令人信服,受到伏爾泰(Voltaire)的無情嘲諷。這或許使得拉格朗日將1788年的“分析力學”建立在達朗貝爾原理的基礎上而非最小作用原理的基礎上,儘管他早在1760年對這一原理已有了相當明確的一般數學提法。很晚以後,哈密頓(Hamilton,W.R.)和雅可比才給這一原理以令人滿意的形式,大概是亥姆霍茲(Helmholtz,H.von)把它提高到最普遍的物理規律的行列.20世紀前半期,物理學家主要熱衷於用空間時間微分方程描述自然規律,最小作用原理又明顯回潮。
