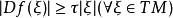拓撲穩定性(topological stability)亦稱半結構穩定性或半穩定性，通常是描述系統在C小擾動下的一個穩定性概念。
對於自映射情形，也可給出拓撲穩定性的類似定義。微分流形上的安諾索夫系統是拓撲穩定的；擴張映射是拓撲穩定的。對微分同胚來說，公理A和強橫截條件蘊涵著拓撲穩定性。
基本介紹
- 中文名：拓撲穩定性
- 外文名：topological stability
- 領域：數學
- 別稱：半結構穩定性或半穩定性
- 性質：系統在小擾動下的穩定性
- 實例：擴張映射
概念,穩定性,度量空間,同胚,實例——擴張映射,
概念
拓撲穩定性(topological stability)亦稱半結構穩定性或半穩定性。
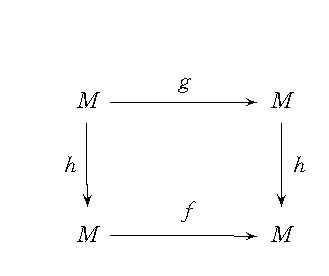
通常是描述系統在C小擾動下的一個穩定性概念。設(M，d)是緊緻度量空間，f：M→M是同胚。若對任意ε>0，存在δ>0，使得對任意同胚g：M→M，當d(f，g)≤δ時，存在連續滿射h：M→M滿足：
1.h°g=f°h，即上圖可交換；
2.d(h，idM)≤ε；
則稱f是拓撲穩定的。
對度量空間上的連續流而言，其定義如下：設(M，d)是緊緻度量空間，φ是M上的連續流。若對任意ε>0，存在δ>0，使得對任意連續流ψ：R×M→M及任t∈(0，1]，當d(φt，ψt)≤δ時，存在連續滿射h：M→M滿足：
1.對任意x∈M，h把φ過x的軌道映到ψ過h(x)的軌道內；
2.d(h，idM)≤ε；
則稱φ是拓撲穩定的。
對於自映射情形，也可給出拓撲穩定性的類似定義。微分流形上的安諾索夫系統是拓撲穩定的；擴張映射是拓撲穩定的。對微分同胚來說，公理A和強橫截條件蘊涵著拓撲穩定性。
穩定性
一般是指作用在系統上的擾動排除後，系統能否恢復原狀、或以怎樣的精度恢復原狀的性能。它是控制理論的一個極其重要的問題。在經典控制理論中，一般涉及到的是定常的線性系統，有關這種系統的穩定性的判別方法主要有： 羅斯—胡爾維茨準則、奈奎斯特判據、波德圖、尼柯爾圖和根軌跡法等。在現代控制理論中，對線性系統和非線性系統的穩定性的研究，主要是李雅普諾夫的穩定性理論。李雅普諾夫根據系統的輸出 (回響) 是否有界來定義系統的穩定性，並區分了三種情況： (1) 穩定的，即對於系統初始值的一個擾動，如果其回響的幅值是有界的。(2) 漸近穩定的，即對於系統初始值的一個擾動，如果其回響能夠最終回到初始狀態。(3)不穩定的，即對於系統初始值的一個擾動，其回響的幅值不是有界的。經典控制理論所研究的穩定性只限於第二種情況漸近穩定，而把另兩種情況都看作是不穩定的。因而李雅普諾夫的穩定性概念更具一般性。李雅普諾夫用兩種方法分析系統的穩定性，第一種方法是： 用近似極數表示非線性函式，然後用近似方法求解非線性方程，最後根據解的性質，確定其系統的穩定性; 第二種方法是： 不必求解方程，而用李雅普諾夫函式的純量函式來判別系統是否穩定，並分析系統的回響。由於第二種方法具有不必求解方程的特點，因而也稱直接法，而稱第一種方法為間接法。由於許多非線性系統和時變系統的方程是難以求解的，又由於通過計算機可以找到所需的李雅普諾夫函式，還能找到系統的穩定區域，所以第二種方法在控制理論中得到廣泛套用。穩定性對於社會經濟系統極為重要，是經濟學經常討論的重要課題之一。探討經濟系統的穩定性，對於了解經濟系統的動態發展規律、預測經濟發展方向以及分析經濟系統的結構等，都有著重要的現實意義。
度量空間
度量空間亦稱距離空間。一種拓撲空間，其上的拓撲由距離決定。設R是一個非空集合，ρ(x，y)是R上的二元函式，滿足如下條件：
1.ρ(x，y)≥0且ρ(x，y)=0⇔x=y;
2.ρ(x，y)=ρ(y，x);
3.(三角不等式)ρ(x，y)≤ρ(x，z)+ρ(y，z);
則稱ρ(x，y)為兩點x，y之間的距離，R按距離ρ成為度量空間或距離空間，記為(R，ρ)。設A是R的子集，則A按R中的距離ρ也成為度量空間，稱為R的(度量)子空間。如果把上述距離的條件1改為ρ(x，y)≥0且ρ(x，x)=0，則稱ρ為R上的擬距離。當ρ(x，y)=0時，記x～y.～是R上的一個等價關係，記商集(即等價類全體)為D=R/～，在D上作二元函式ρ～：ρ～(x～，y～)=ρ(x，y)(x∈x～，y∈y～)，則ρ～是D上的距離，而(D，ρ～)稱為R按擬距離ρ導出的商(度量)空間。
度量空間(R，ρ)中的子集A稱為有界的，如果對x0∈R，存在常數M，使ρ(x0，x)≤M對A中的一切x成立。設x0∈R，r>0，則稱集合{x|x∈R，ρ(x，x0)<r}為以x0為中心，r為半徑的開球，或x0的r鄰域，記為O(x0，r).又設A⊂R，若對任何x∈A，存在x的某個鄰域O(x，r)⊂A，則A稱為開集;而稱開集的補集為閉集。R中包含子集A的最小閉集就稱為A的閉包。
同胚
數學上指一對一的一種對應。在集合論(set theory)中指兩組成員的一種屬性，一組中的任何一個成員能同另一組中的一個成員配對，反之亦然。在拓撲學(topology)中，兩個空間中的一個能不撕破、不粘連地變形成另一個，這兩個空間就是同胚的。例如，球體的表面和立方體的表面就是同胚的。
設E與F為兩個拓撲空間。稱從E到F上的雙射為從E到F上的同胚，如果這一映射能建立一個從E之全體開集的集合到F之全體開集的集合上的雙射。
為使從E到F上的雙射是同胚，其充分必要條件是： 這個雙射是雙連續的。
實例——擴張映射
撒布(Shub，M.)在1969年最先研究得到的一類結構穩定的半動力系統。最簡單的擴張映射的例子是複平面上由z↦z2定義的單位圓周的自映射。一般定義是：設M是緊緻黎曼流形，f∈C1(M，M)，如果存在M上的黎曼度量〈·，·〉和實數τ>1，使得：
