基本介紹
- 中文名:費馬原理
- 外文名:Fermat's principle
- 學科領域:幾何光學
- 用途:光學、地震學
定義
- 光線在真空中的直線傳播。
光的反射
平面反射










半球面反射






運動學
參閱
- 惠更斯-菲涅耳原理
















費馬原理(Fermat's principle)最早由法國科學家皮埃爾·德·費馬在1662年提出:光傳播的路徑是光程取極值的路徑。這個極值可能是最大值、最小值,甚至是函式的拐點...
費馬大定理,又被稱為“費馬最後的定理”,由17世紀法國數學家皮耶·德·費瑪提出。他斷言當整數n >2時,關於x, y, z的方程 x^n + y^n = z^n 沒有正...
惠更斯-菲涅耳原理(英語:Huygens–Fresnel principle)是研究波傳播問題的一種分析方法,因荷蘭物理學者克里斯蒂安·惠更斯和法國物理學者奧古斯丁·菲涅耳而命名。這個原理...
物理學中 最小作用量原理(英語:least action principle),或更精確地,平穩作用量原理(英語:stationary action principle),是一種變分原理,當套用於一個機械系統的...
這種方法是世界上最古老的一種求質數的方法,它的原理很簡單,運用起來也很方便....17世紀時,有個法國律師叫費馬(Fermat,1601-1665),他非常喜歡數學,常常利用業餘...
費馬(Fermat)引理是實分析中的一個定理,以皮埃爾·德·費馬命名。通過證明函式的每一個極值都是駐點(函式的導數在該點為零),該定理給出了一個求出可微函式的...
出版信息光學原理(第2版) 作者:沈常宇、金尚忠 定價:45元 印次:2-1 ISBN:9787302470151 出版日期:2017.09.01 印刷日期:2017.08.07 內容簡介本書系統地闡述了...
在物理學裡,最小作用原理,即最小作用量原理(英語:least action principle),或更精確地,平穩作用量原理(英語:stationary action principle),是一種變分原理,當套用...
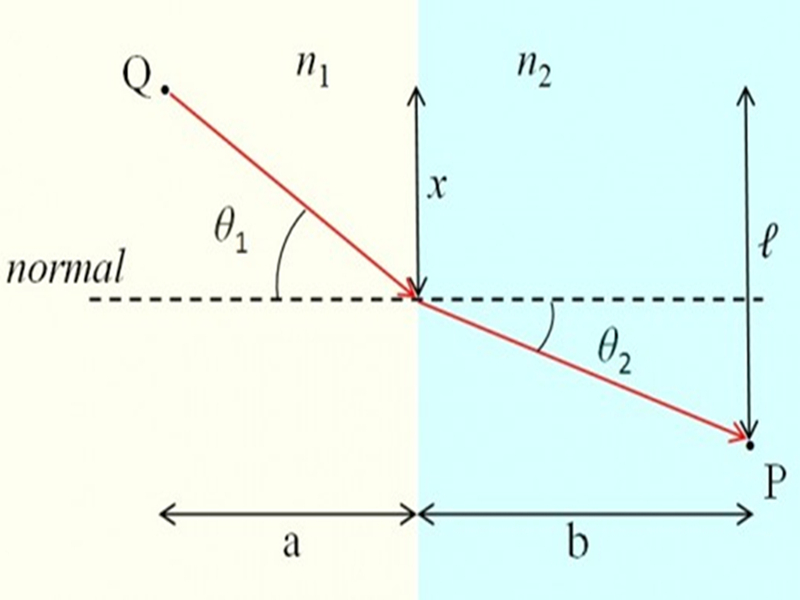
從費馬原理,可以推導出斯涅爾定律。通過設定光程對於時間的導數為零,可以找到“平穩路徑”,這就是光線傳播的路徑。光線在介質1與介質2的傳播速度分別為v1=c/n1,...
折射角用費馬原理推導 費馬原理又稱為“最短時間原理”:光線傳播的路徑是需時最少的路徑。費馬原理更正確的版本應是“平穩時間原理”。對於某些狀況,光線傳播的...
法國人費馬(1601—1665)從理論上得到費馬原理,並用演繹方法從費馬原理中推導出折射定律。1.費馬從理論上得到費馬原理.費馬從理論上推導出:光沿著光程為極值的路徑...
