基本介紹
- 中文名:費馬引理
- 外文名:Fermat's theorem
- 別稱:Fermat引理
- 提出者:皮埃爾·德·費馬
- 套用學科:數學
- 適用領域範圍:微積分
陳述,證明,方法1,方法2,
費馬(Fermat)引理是實分析中的一個定理,以皮埃爾·德·費馬命名。通過證明函式的每一個極值都是駐點(函式的導數在該點為零),該定理給出了一個求出可微函式的...
費馬大定理,又被稱為“費馬最後的定理”,由17世紀法國數學家皮耶·德·費瑪提出。他斷言當整數n >2時,關於x, y, z的方程 x^n + y^n = z^n 沒有正...
廣義費馬定理是費馬定理的一種推廣。實則把費馬小定理從整數範圍推廣到整係數多項式的集合中而得到。...
《從費馬到懷爾斯:費馬大定理的歷史》介紹了關於費馬大定理的歷史,並詳細介紹了證明費馬大定理的艱難歷程。主要分為三部分:上篇攻克費馬大定理的歷程、中篇費馬對...
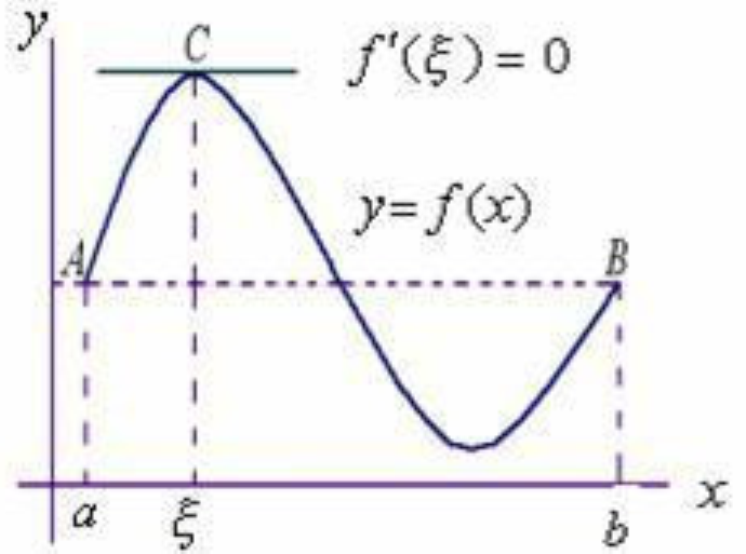
至少有一個在 (a,b) 內某點ξ處取得,從而ξ是f(x)的極值點,又條件 f(x) 在開區間 (a,b) 內可導得,f(x) 在ξ 處取得極值,由費馬引理推知:f'(...
世界三大數學猜想即費馬猜想、四色猜想和哥德巴赫猜想。費馬猜想的證明於1994年由英國數學家安德魯·懷爾斯(Andrew Wiles)完成,遂稱費馬大定理;四色猜想的證明於1976年...
