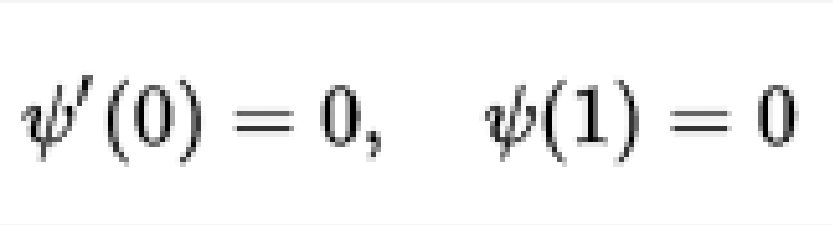在數學中,劉維爾方程(Liouville equation),又稱劉維 - 布拉-蓋爾芬德方程(Liouville-Bratu-Gelfand equation)是一個非線性特徵值泊松方程,以數學家約瑟夫·劉維爾(Joseph Liouville)、布拉圖和以色列格爾芬德命名。方程式為:▽2ψ+λeψ=0
此方程式出現在弗蘭克 - Kamenetskii理論的熱失控中以及錢德拉塞卡方程的天體物理學中。 這個方程還描述了發光線周圍的空間電荷,並描述了行星狀星雲。
基本介紹
- 中文名:劉維爾方程
- 外文名:Liouville equation
- 學科:數學
- 別稱:劉維 - 布拉-蓋爾芬德方程
- 本質:非線性特徵值泊松方程
- 提出者:約瑟夫·劉維爾
定義
劉維爾方程解
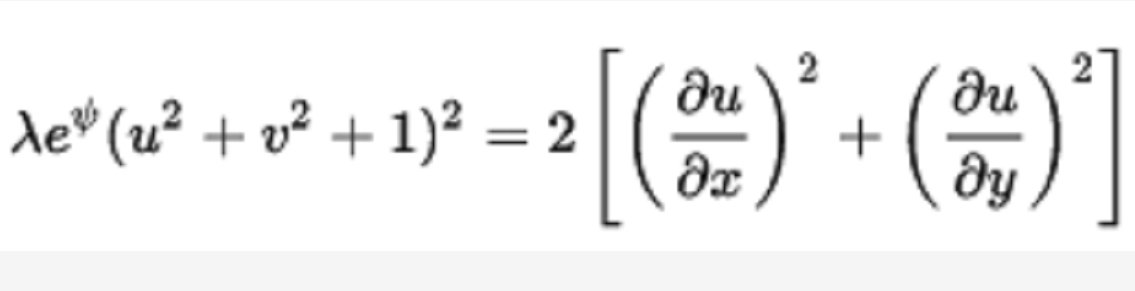


徑向對稱形式