施圖姆-劉維爾問題,即施圖姆-劉維爾理論,在數學及其套用中,以雅克·夏爾·弗朗索瓦·施圖姆(1803–1855)和約瑟夫·劉維爾(1809–1882)的名字命名,具體定義見正文。
基本介紹
- 中文名:施圖姆-劉維爾問題
- 外文名:Sturm–Liouville theory
- 別稱:施圖姆-劉維爾理論
簡介
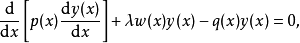


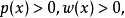
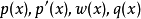
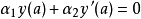
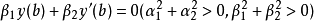



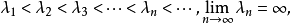
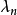



一些函式的施圖姆-劉維爾形式
貝塞爾方程
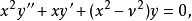
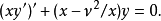
勒讓德方程
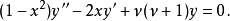
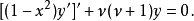
使用積分因子的例子
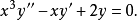
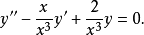
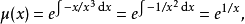
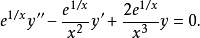
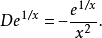
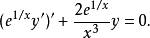
一般形式二階常微分方程的積分因子
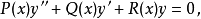
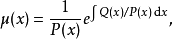
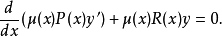
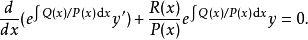
施圖姆-劉維爾問題,即施圖姆-劉維爾理論,在數學及其套用中,以雅克·夏爾·弗朗索瓦·施圖姆(1803–1855)和約瑟夫·劉維爾(1809–1882)的名字命名,具體定義見正文。
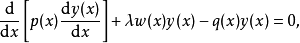


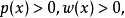
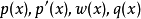
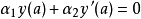
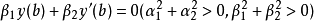



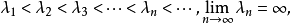
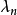



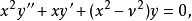
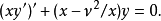
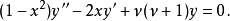
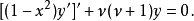
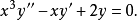
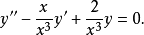
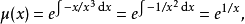
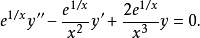
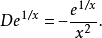
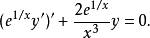
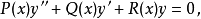
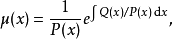
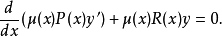
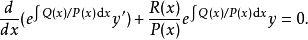
施圖姆-劉維爾問題,即施圖姆-劉維爾理論,在數學及其套用中,以雅克·夏爾·弗朗索瓦·施圖姆(1803–1855)和約瑟夫·劉維爾(1809–1882)的名字命名,具體定義見正文。....
5.4 正則施圖姆-劉維爾問題1105.5 振動理論1145.6 周期施圖姆-劉維爾方程119第2部分 動力系統第6章 動力系統1276.1 動力系統127...
3.2 施圖姆-劉維爾型方程的特徵值問題3.2.1 施圖姆-劉維爾型方程的形式3.2.2 施圖姆-劉維爾方程的邊界條件3.2.3 施圖姆-劉維爾特徵值問題...
從基本的常微分方程向更多高級概念(偏微分方程、傅立葉級數和邊界值問題等)順利...6.4四階施圖姆-劉維爾理論6.5梁的彈性振動和屈曲6.6雙調和運算元6.7圓盤的振動...
8.3 正則施圖姆——劉維爾特徵值問題8.4 非齊次定解問題的處理8.5 二維拉普拉斯方程的邊值問題8.6 高維空間有界區域上的偏微分方程定解問題概述...
為求解方便一般也寫成如下施圖姆-劉維爾形式(Sturm-Liouville form):上述方程及其...當試圖在球坐標中求解三維拉普拉斯方程(或相關的其他偏微分方程)時,問題便會歸...
10.2施圖姆一劉維爾本徵值問題習題10第11章波動方程的達朗貝爾解11.1弦振動方程的達朗貝爾解11.2三維空間的行波法推遲勢習題11第12章格林函式法...
本書系統介紹偏微分方向的基本概念及其套用,主要內容包括熱傳導方程、分離變數法、傅立葉級數、施圖姆一劉維爾特徵值問題、偏微分方程的有限差分數值法、非齊次問題...
6.2.1施圖姆 劉維爾方程6.2.2本徵值問題的一般提法6.2.3本徵值問題的一般性質習題6第7章貝塞爾函式及其套用7.1貝塞爾方程的引入...
全書內容分為10章,分別介紹矢量分析與場論的基礎知識、數學物理定解問題的推導、...2.3.2施圖姆-劉維爾問題 ... 212.3.3例子...
6.5 施圖姆-劉維爾問題歷史註記:傅立葉歷史註記:狄利克雷套用詳析:量子力學中的一些思想分類習題第7章 拉普拉斯變換7.1 引言7.2 套用於微分方程...
