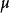對於微分方程M(x,y)dx+N(x,y)dy=0,如果存在連續可微函式μ(x,y),可以使μMdx+μNdy=0成為恰當方程,即μMdx+μNdy=du,則稱μ為該微分方程的積分因子。求解積分因子的常用方法主要由觀察法、積分法和分組法。
基本介紹
- 中文名:積分因子
- 外文名:integrating factor
- 套用:將非恰當方程化為恰當方程
定義,存在性,確定方法,觀察法,積分法,分組法,
定義
由於恰當方程可以比較方便的求出通解,於是人們想到能否將一非恰當方程化為恰當方程呢?由此就引入了積分因子的概念。
如果存在連續可微函式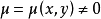 ,使得
,使得
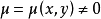

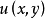

則稱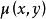 為方程
為方程 的積分因子。這時
的積分因子。這時 即為方程
即為方程 的通解,因而也就是方程
的通解,因而也就是方程 的通解。
的通解。
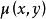




存在性
可以證明,只要方程 有解存在,則必有積分因子存在,且不是唯一的。
有解存在,則必有積分因子存在,且不是唯一的。

事實上,設該方程有通解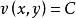 ,對其微分可得
,對其微分可得
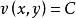


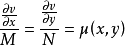

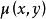
例如, 可以取
可以取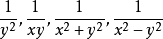 中的任何一個函式作為積分因子。
中的任何一個函式作為積分因子。

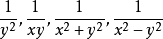
確定方法
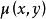
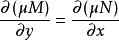

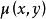
觀察法
對於某些比較簡單的微分方程,藉助常用的全微分公式,可以直接寫出方程的積分因子。如上面所說的 可以取
可以取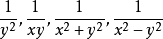 中的任何一個函式作為積分因子。
中的任何一個函式作為積分因子。

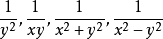
積分法
設方程 存在積分因子
存在積分因子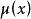 ,則方程
,則方程 變為
變為 ,因為
,因為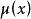 與
與 無關,所以方程有解的充要條件是:
無關,所以方程有解的充要條件是: 僅與
僅與 有關。設
有關。設 ,則
,則

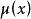


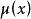







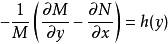
從而

分組法
如果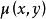 是方程的一個積分因子,使得
是方程的一個積分因子,使得 ,則
,則 也是該方程的一個積分因子,其中
也是該方程的一個積分因子,其中 是
是 的任一可微非零函式。
的任一可微非零函式。
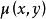




利用上述定理使分組求積分因子的方法一般化。如果方程左端可以分成兩組,即
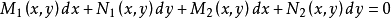
設兩組分別有積分因子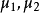 使得
使得
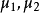


則 是第一組的積分因子,
是第一組的積分因子, 是第二組的積分因子。如果能找到適當的可微函式
是第二組的積分因子。如果能找到適當的可微函式 ,使得
,使得 ,那么
,那么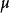 就是所找的積分因子。
就是所找的積分因子。