高斯-盧卡斯定理

高斯-盧卡斯定理，又稱盧卡斯定理，該定理描述了復係數多項式的一個性質：多項式導數的根一定在原多項式的根所構成的凸包內。

這一結論曾在1836被Carl Friedrich Gauss直接使用，1874 得到證明。

基本介紹

• 中文名：高斯-盧卡斯定理
• 外文名：Gauss–Lucas theorem
• 分類：數理科學

動機

我們注意到，二次多項式 的導數的根為原多項式的兩個根的平均數。

同樣地，如果一個次多項式有個兩兩不同的實值零點，根據羅爾定理，其導數的每個零點都位於區間之中。

高斯-盧卡斯定理可以看成這一性質在復係數多項式上的推廣。

表述

設 是一個非常數的復係數多項式，那么所有的根屬於的根構成的凸包。

證明

將多項式函式P寫成複數下的不可約形式： ，其中複數是多項式的主係數、是多項式的根、 為各個根的重數。

首先注意到：

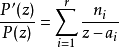
假設複數滿足：

因此：

乘以共軛取模：

寫成如下形式：

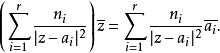
此時，我們可以將看成是個位於的質點的重心，因此在其構成的凸包內。

另一種情況下的證明是顯然的。