基本介紹
- 中文名:羅爾中值定理
- 外文名:Rolle's theorem
- 別稱:羅爾定理
- 提出時間:1691年
- 套用學科:高等數學 微分學
- 適用領域範圍:物理、數學等
- 適用領域範圍:方程根的存在性
證明過程
幾何意義
幾種特殊情況


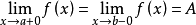









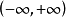

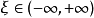


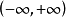
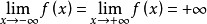

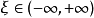


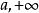




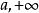





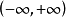

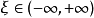


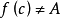

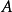







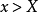


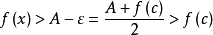

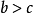





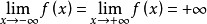
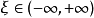



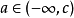


羅爾定理一般指本詞條


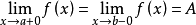









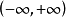

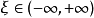


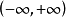
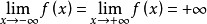

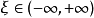


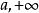




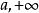





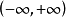

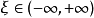


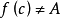

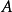







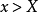


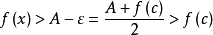

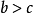





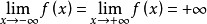
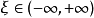



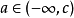

羅爾(Rolle)中值定理是微分學中一條重要的定理,是三大微分中值定理之一,其他兩個分別為:拉格朗日(Lagrange)中值定理、柯西(Cauchy)中值定理。羅爾定理描述如下:...
拉格朗日中值定理又稱拉氏定理,是微分學中的基本定理之一,它反映了可導函式在閉區間上的整體的平均變化率與區間內某點的局部變化率的關係。拉格朗日中值定理是羅...
拉格朗日定理微積分 編輯 在微積分中,拉格朗日中值定理是羅爾中值定理的推廣,同時也是柯西中值定理的特殊情形。1.文字敘述如果函式 滿足:1) 在閉區間 上連續;2)...
微分中值定理羅爾定理 編輯 內容:如果函式f(x)滿足:在閉區間[a,b]上連續;在開區間(a,b)內可導;在區間端點處的函式值相等,即f(a)=f(b),...
微分中值定理主要包括羅爾定理、拉格朗日定理、柯西定理、泰勒定理,其中羅爾定理是拉格朗日定理等的預備定理,由三個已知條件推得結果,三個已知條件缺一不可,即若要...
柯西(Cauchy) 中值定理是微分中值定理的三大定理之一,它比羅爾(Rolle) 定理與拉格朗日(Lagrange) 中值定理更具一般性,也具有更廣泛的套用性,但大多高等數學的...
在一元函式微分學中,微分中值定理是套用函式的局部性質研究函式在區間上整體性質的重要工具,它在數學分析中占有重要的地位,其中拉格朗日中值定理是核心,羅爾定理是...
,根據羅爾定理,其導數的每個零點都位於區間 之中。高斯-盧卡斯定理可以看成這一性質在復係數多項式上的推廣。高斯-盧卡斯定理表述 編輯 設 是一個非常數的復係數...
米歇爾·羅爾(Michel Rolle,1652年4月21日-1719年11月8日),是法國數學家。他著名的有羅爾定理(1691年)。他也發明了現在的標準記法以表示x的n次根。...
勒文海姆-斯科倫定理羅爾定理拉格朗日定理 (群論)拉格朗日中值定理拉姆齊定理拉克斯-米爾格拉姆定理黎曼映射定理呂利耶定理勒讓德定理拉格朗日定理 (數論)勒貝格微分定理...
微分中值定理反映了導數的局部性與函式的整體性之間的關係,套用十分廣泛。微分中值定理包括羅爾定理、拉格朗日定理、柯西定理、泰勒公式、達布定理、洛必達法則等。...
3.2 羅爾定理的證明//523.3 最大、最小值定理的證明//553.4 最大最小值定理的背景及推廣//66第4章 中值定理的推廣//74...
在微積分學的理論證明中,中值定理具有根本的重要性,它有許多不同的形式。微分學羅爾定理 1690年法國數學家M.羅爾首先發現,在閉區間上連續,區間內可微,在區間...
