基本介紹
- 中文名:最大值
- 外文名:The maximum value
- 歸屬學科:數學
- Matlab:MAX()函式
- 基本釋義:已知數據中的最大的值
- 存在充要條件:函式f在[a,b]上連續
介紹
存在性

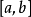

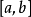
一般求解方法
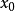
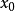
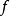
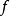
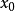
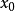
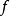
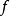
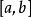
示例


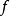

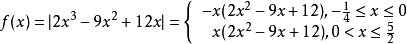



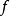
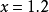


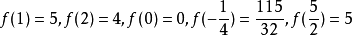
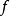

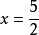
方法
換元法求最值

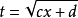


判別式求最值
函式單調性
數形結合
求導方法
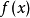
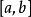
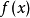
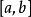
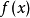




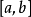

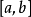
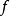
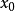
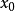
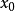
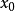
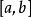


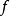

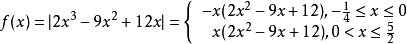



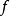
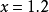


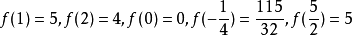
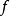

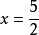

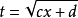


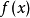
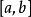
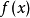
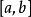
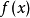


最大值,即為已知的數據中的最大的一個值,在數學中,常常會求函式的最大值,一般求解方法有換元法、判別式求法、函式單調性求法、數形結合法和求導方法。...
函式最大值即函式在定義域內的最大數值。...... )是函式f(x)的最大值;若存在x0∈R,使得對任意的x∈R,有f(x)≤f(x0),則f(x0)是函式f(x)的最大...
最優控制中的最大值原理,是在目標泛函的最大化問題中得到最優控制的必要條件是使哈密頓函式達最大值而得名的。它被廣泛套用於開放式捕魚以及日常實際問題求最優...
《最大值計算器》是一款用於計算出最大值的程式。...... 圖集 最大值計算器圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建...
年超大值法簡介 暴雨選樣通常分為年最大值法和非年最大值法。非年最大值法又分為年超大值法、超定量法及年多個樣法。 年超大值法是將N年中的各歷時全部...
《愛的最大值》是最後的朝日E1系創作的網路小說,發表於晉江文學網。...... 《愛的最大值》是最後的朝日E1系創作的網路小說,發表於晉江文學網。 ...
函式在某個極小區間內,存在自變數取值x,且存在比其大與比其小的自變數,這些自變數所對應的函式值均小於x對應的函式值。那么此函式值稱為極大值。即若對點x0的...
函式的最大值(maximum of a function)亦稱函式的絕對極大值或整體極大值.函式值所能取到的最大者。...
過程差最大值,汽車在制動過程中制動力增長全過程到車輪抱死程度(滑移率)到達20%時產生最大的制動效果的那一點。...
極大值原理是對分析力學中古典變分法的推廣,能用於處理由於外力源的限制而使系統的輸入(即控制)作用有約束的問題。極大值原理是20世紀50年代中期蘇聯學者Л.С....
一般的,函式最值分為函式最小值與函式最大值。簡單來說,最小值即定義域中函式值的最小值,最大值即定義域中函式值的最大值。函式最大(小)值的幾何意義——...
最大回撤率:在選定周期內任一歷史時點往後推,產品淨值走到最低點時的收益率回撤幅度的最大值。最大回撤用來描述買入產品後可能出現的最糟糕的情況。最大回撤...
PS【最大值】命令可以對可以對畫面中的亮區進行擴大,對畫面中的暗區進行縮小。在指定的半徑中,軟體搜尋像素中的最大值並利用該像素替換其他的像素。 ...
最大升阻比是升阻比的最大值。升阻比是指飛行器在飛行過程中,在同一迎角的升力與阻力(也即升力係數與阻力係數)的比值。其值與飛行器迎角、飛行速度等參數有關,...
複變函數論中有關函式值的模的一個重要而有用的定理,斷言解析函式的模在區域內部不能達到極大值,除非它是常數函式。這一原理可具體表述如下:設ƒ(z)為有界...
在數學分析中,函式的最大值和最小值(最大值和最小值)被統稱為極值(極數),是給定範圍內的函式的最大值和最小值(本地 或相對極值)或函式的整個定義域(全局...
在數學分析中,在給定範圍內(相對極值)或函式的整個域(全局或絕對極值),函式的最大值和最小值被統稱為極值(極數)。皮埃爾·費馬特(Pierre de Fermat)是第一位...
設minA和maxA分別為屬性A的最小值和最大值,將A的一個原始值v通過min-max標準化映射成在區間[new_minA, new_maxA]中的值v’。...
在數學分析中,函式的最大值和最小值(最大值和最小值)被統稱為極值(極數),是給定範圍內的函式的最大值和最小值(本地 或相對極值),給定函式的整個定義域的...
基本不等式是主要套用於求某些函式的最值及證明的不等式。其表述為:兩個正實數的算術平均數大於或等於它們的幾何平均數。...
極差又稱範圍誤差或全距(Range),以R表示,是用來表示統計資料中的變異量數(measures of variation),其最大值與最小值之間的差距,即最大值減最小值後所得之...
注意:這裡我們通過對拉格朗日乘數的解釋考查了cj的微小變動dcj對目標函式最大值的變化的影響,這就是開篇所說的比較靜態研究—研究參數θ的變化對最大值的影響。...
胸徑:又稱乾徑,指喬木主幹離地表面胸高處的直徑,斷面畸形時,測取最大值和最小值的平均值。不同的喬木的胸高有差異,不同的國家對胸徑的規定也有差別。我國和...
