k階中值定理

k階中值定理是微分中值定理的推廣。

基本介紹

• 中文名：k階中值定理
• 外文名：mean value theorem of order k
• 適用範圍：數理科學

簡介

k階中值定理是微分中值定理的推廣。

若f:[a,b]→R在[a,b]上k次可微，h=(b-a)/k，則存在ξ∈(a,b)，使。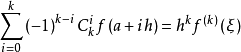

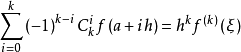
套用

如果函式f二階連續可微，即∇²f(x)存在且連續，那么就有二階Taylor展開和二階中值定理。

特別地，對任意x和y有f(x+y)=f(x)+y'∇f(x)+0.5y'∇²f(x)y+o(|lyll²)，同時存在α∈[0,1]，使得f(x+y)=f(x)+y'∇f(x)+0.5∇²f(x+αy)y。

微分中值定理

微分中值定理是一系列中值定理總稱，是研究函式的有力工具，其中最重要的內容是拉格朗日定理，可以說其他中值定理都是拉格朗日中值定理的特殊情況或推廣。微分中值定理反映了導數的局部性與函式的整體性之間的關係，套用十分廣泛。

微分中值定理包括羅爾定理、拉格朗日定理、柯西定理、泰勒公式、達布定理、洛必達法則等。