基本介紹
- 中文名:洛必達法則
- 外文名:L'Hopital's rule
- 一般定義:確定未定式值的一種特殊方法
- 學科分類:數學、微積分
- 創立時間:1696年
- 提出人物:洛必達
- 運算特點:分子、分母同時求導
計算公式
零比零型



無窮比無窮型
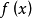

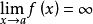

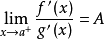
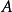

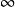

其他不定式
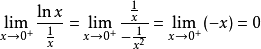





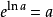
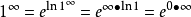
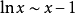



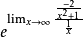

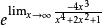
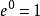

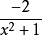

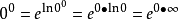

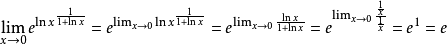
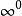
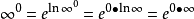


定理推廣
 圖1 法國數學家-洛必達
圖1 法國數學家-洛必達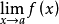
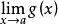
套用條件
注意事項

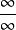




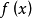

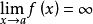

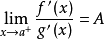


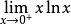
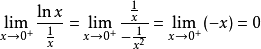





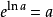
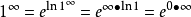
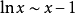



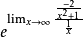

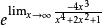
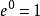

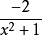

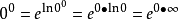

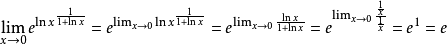
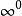
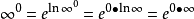


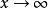
 圖1 法國數學家-洛必達
圖1 法國數學家-洛必達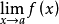
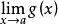

洛必達法則是在一定條件下通過分子分母分別求導再求極限來確定未定式值的方法。眾所周知,兩個無窮小之比或兩個無窮大之比的極限可能存在,也可能不存在。因此,求...
洛必達(Marquis de l'Hôpital,1661-1704),)又音譯為羅必塔(L'Hôpital)法國的數學家,偉大的數學思想傳播者。...
柯西中值定理的一個最重要的套用就是可以推導計算待定型的極限最有效的方法——洛必達法則。洛必達法則是求兩個無窮小量或兩個無窮大量的比的極限。在滿足一定...
洛必達法則 別名 L'Hôpital Rule 條件 不能用商的極限等於極限的商來求 目錄 1 定義 2 分類 未定式定義 編輯 如果當x→x0(或者x→∞)時,兩個函式...
值與導數值之間的定量聯繫,因而可用中值定理通過導數去研究函式的性態;中值定理的主要作用在於理論分析和證明;同時由柯西中值定理還可導出一個求極限的洛必達法則...
洛必達法則(L'Hospital):是在一定條件下通過分子分母分別求導再求極限來確定未定式值的方法。設(1)當x→a時,函式f(x)及F(x)都趨於零...
與洛必達法則的疊代用法類似,在嘗試套用斯托爾茲-切薩羅定理考察數列的極限時,如果發現兩個數列差分的商仍然是不定型,可以嘗試再使用1次該定理,考察其2階差分之...
可利用拉格朗日中值定理對洛必達法則進行嚴格的證明,並研究泰勒公式的餘項。從柯西起,微分中值定理就成為研究函式的重要工具和微分學的重要組成部分。 [3] ...
1 羅爾定理 2 拉格朗日定理 3 柯西定理 4 泰勒公式 5 達布定理 6 洛必達法則 微分中值定理羅爾定理 編輯 內容:如果函式f(x)滿足:在...
洛必達法則 法國數學家 G.-F.-A de洛必達於1696年在他的名著《無窮小分析》中,給出了一種確定未定式值的方法:如果函式ƒ(x)與g(x)在區間(α,b)內...
分式極限,分子趨不趨於無窮大無所謂)、0/0型極限(此時要求分子分母都以0為極限)。O'Stolz定理用於數列,它有函式形式的推廣,這兩個都可以認為是洛必達法則的...
④採用洛必達法則求極限洛必達法則是分式求極限的一種很好的方法,當遇到分式0/0或者∞/∞時可以採用洛必達,其他形式也可以通過變換成此形式。...
可以通過洛必達法則求得 目錄 1 意義 2 不定式 0/0意義 編輯 “0/0”稱之為不定式,可以等於任何數。在函式上表示真正的徹底的無意義。 在物理學與工程上...
(2)解這種問題時除了使用洛必達法則外,經常會用到等價無窮小替代及換元方法。冪指函式求導方法 編輯 下面給出一般冪指函式的求導方法。為書寫方便,把f(x)和g...
解 作倒代換 ,原式 ,使用洛必達法則可得到如果使用麥克勞林展開式,則計算更為簡單倒代換解積分問題 編輯 不定積分問題對於不定積分問題來說,當被積函式是分母...
(以上幾個性質可以用來化簡一些未定式以方便運用洛必達法則)需要滿足一定條件才能替換的類型若 ,則(該條性質非常重要,這是判斷在加減法中能否分別等價替換的重要...
例如解決懸鏈線問題(1691年),提出洛必達法則(1694年)、最速降線(1696年)和測地線問題(1697年),給出求積分的變數替換法(1699年),研究弦振動問題(1727年),出版...
例如解決懸鏈線問題(1691年),提出洛必達法則(1694年)、最速降線(1696年)和測地線問題(1697年),給出求積分的變數替換法(1699年),研究弦振動問題(1727年),出版...
