基本介紹
- 中文名:等價無窮小
- 外文名:equivalent infinitesimal
- 別稱:等價無窮小量
- 表達式:lim a/b=lim a'/b'
- 提出者:阿基米德
- 提出時間:公元前300年
- 套用學科:高等數學
- 適用領域範圍:求極限
定義
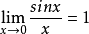

- 被代換的量,在取極限的時候極限值為0;
- 被代換的量,作為被乘或者被除的元素時可以用等價無窮小代換,但是作為加減的元素時就不可以。
定理
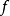
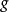

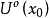
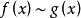


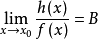
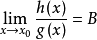
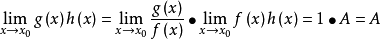
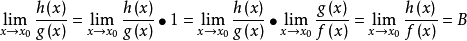
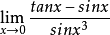
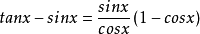
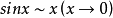
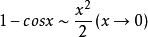
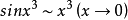
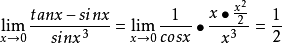
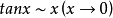
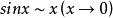
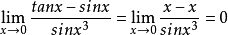
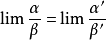
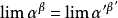
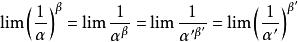
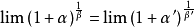
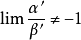
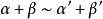
公式
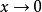
 常見等價無窮小
常見等價無窮小
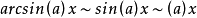
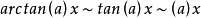
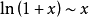
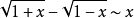

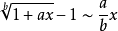
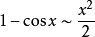
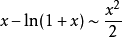
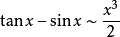
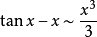
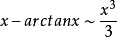
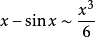

推導過程

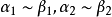
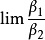
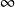
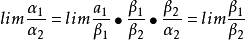

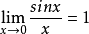

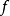
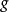

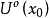
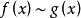


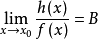
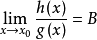
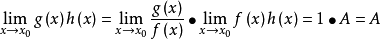
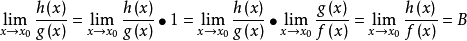
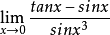
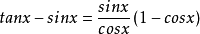
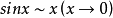
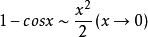
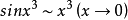
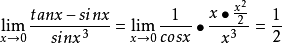
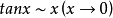
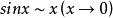
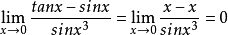
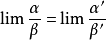
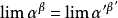
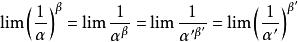
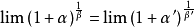
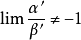
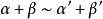
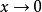
 常見等價無窮小
常見等價無窮小
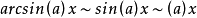
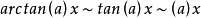
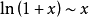
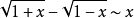

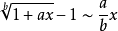
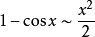
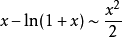
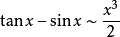
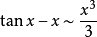
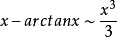
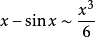


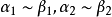
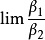
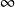
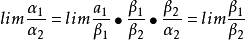
無窮小就是以數零為極限的變數。然而常量是變數的特殊一類,就像直線屬於曲線的一種。因此常量也是可以當做變數來研究的。這么說來——0是可以作為無窮小的常數。從...
等價無窮小量指的是在兩個無窮小量在極限運算過程中等價代換。它對於極限的求解起到簡便運算作用。...
無窮小量是數學分析中的一個概念,在經典的微積分或數學分析中,無窮小量通常以函式、序列等形式出現。1無窮小量即以數0為極限的變數,無限接近於0。確切地說,當...
型”待定型,先求 ,其中利用等價無窮小關係公式 可作等價無窮小代換 ,即可得所以 。(3)求解 這個極限式是“ 型”待定型,先求 待定型 ,根據洛必達法則可得所...
洛必達法則是在一定條件下通過分子分母分別求導再求極限來確定未定式值的方法。眾所周知,兩個無窮小之比或兩個無窮大之比的極限可能存在,也可能不存在。因此,求...
對於形如 的極限問題,很難使用等價無窮小替代和展開泰勒公式,而等價無窮小替代和展開泰勒公式是求極限問題最有效的基本方法。在變數代換 下 ,可能給使用等價無窮小...
【第4條】等價無窮小口訣:(1)有傘即是無傘(傘即sin的諧音,該口訣表示無窮小量的正弦等價於無窮小量本身,也就是可以去掉sin,有sin和無sin是一回事);(2)該...
8.理解無窮小量、無窮大量的概念,掌握無窮小量的比較方法,會用等價無窮小量求極限.9.理解函式連續性的概念(含左連續與右連續),會判別函式間斷點的類型....
8.理解無窮小量、無窮大量的概念,掌握無窮小量的比較方法,會用等價無窮小量求極限.9.理解函式連續性的概念(含左連續與右連續),會判別函式間斷點的類型....
2)消去分母中極限為零的因子(有理化,等價無窮小代換);3)利用無窮小量與有界變數之積為無窮小量 [2] 。【例1】求下列極限(1) ;...
6、用等價無窮小量的代換求極限;7、用洛必達法則求極限;8、用換底公式 求極限。參考資料 1. 王曉萍. 標準編寫中極限數值的表示和判定方法的套用[J]. 中國...
8. 理解無窮小量、無窮大量的概念,掌握無窮小量的比較方法,會用等價無窮小量求極限.9. 理解函式連續性的概念(含左連續與右連續),會判別函式間斷點的類型....
[2017-08-31]. 2. 華夢霞,陳慶. 利用等價無窮小代換求和式極限[J]. 大學數學,2013,29(01):134-137. [2017-08-31]. ...
8.理解無窮小量、無窮大量的概念,掌握無窮小量的比較方法,會用等價無窮小量求極限.9.理解函式連續性的概念(含左連續與右連續),會判別函式間斷點的類型....
無窮小的等價代換241.8 函式的連續性與間斷點25函式在一點處連續定義25函式在開區間上連續26函式在閉區間上連續26函式的間斷點定義26...
等價無窮小的快捷尋找法型未定式極限的快捷計算法型未定式極限的快捷計算法型未定式極限的快捷計算法型未定式極限的快捷計算法參考資料 1. 考研數學三提高與衝刺...
