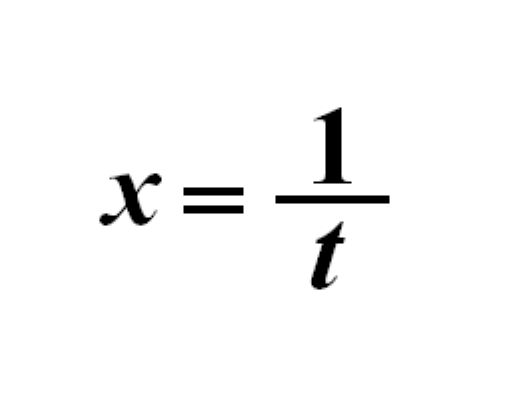倒代換

倒代換是一種通過變數代換x=1/t降低問題難度或化簡解題過程的數學解題方法。

倒代換法常用在極限問題和積分問題的求解過程中。

基本介紹

• 中文名：倒代換
• 外文名：sub back
• 類型：一種數學的解題方法
• 定義：變數代換x=1/t
• 性質：數學名詞

定義

倒代換是通過變數代換 使原來以 為自變數的數學問題變成以 為自變數的數學問題，達到降低問題難度或化簡解題過程的一種數學解題方法。

求極限

對於形如 的極限問題，很難使用等價無窮小替代和展開泰勒公式，而等價無窮小替代和展開泰勒公式是求極限問題最有效的基本方法。

在變數代換 下 ，可能給使用等價無窮小替代、展開泰勒公式，或使用洛必達法則帶來一定的方便

舉例

求極限 。

解 作倒代換 ，原式 ，使用洛必達法則可得到

如果使用麥克勞林展開式，則計算更為簡單

解積分問題

不定積分問題

對於不定積分問題來說，當被積函式是分母次數較高的有理函式或根式有理式時，使用倒代換也許可以使被積函式分母次數變得略低。注意，到計算最後必須把 作回代。

例求不定積分 。

解作倒代換 ，

原式 。

定積分問題

對於定積分問題來說，當被積函式是分母次數較高的有理函式或根式有理式時，使用倒代換也許可以使被積函式分母次數變得略低。但是使用倒代換 時必須特別注意到坐標原點不能包含在積分區間之內。

例1求定積分 。

解作倒代換 ，

原式 。

例2 對於任意實數 ，和任一正實數 ，證明 。

證明 記 ，則在倒代換 下，有

可得 ，證畢。

廣義積分問題

在[ ) 或( ] 上有界函式的廣義積分問題可通過倒代換 變為有界區間上的定積分問題。這樣至少為廣義積分的數值近似計算創造了條件。

例1求 。

解作倒代換 ，

原式 。

例2 通過換元法將廣義積分 轉化為適宜於數值計算的形式

解作倒代換 ，則 ，

對上式第二項作倒代換 ，可得 ,，

這樣就得到了原廣義積分適宜於數值計算的形式