有理函式是通過多項式的加減乘除得到的函式。
在數學中,理性函式是可以由有理分數定義的任何函式,即代數分數,使得分子和分母都是多項式。 多項式的係數不需要是有理數,它們可以在任何欄位K中進行。變數的情況可以在包含K的任何欄位L中進行。函式的域是變數,分母不為零,代碼區為L。
基本介紹
- 中文名:有理函式
- 外文名:Rational function
- 領域:數學
- 涵義:多項式的加減乘除得到的函式
- 屬性:亞純函式
- 分類:擬態函式
介紹
定義

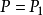
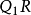

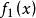
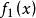
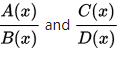

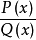
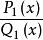
舉例
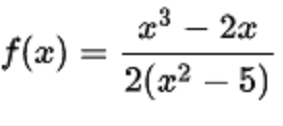
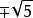
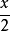


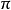

泰勒級數
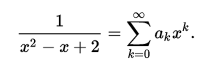
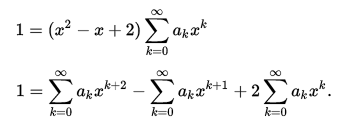


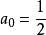
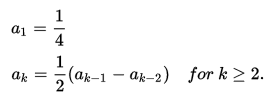
代數和幾何
複雜有理函式

有理函式是通過多項式的加減乘除得到的函式。
在數學中,理性函式是可以由有理分數定義的任何函式,即代數分數,使得分子和分母都是多項式。 多項式的係數不需要是有理數,它們可以在任何欄位K中進行。變數的情況可以在包含K的任何欄位L中進行。函式的域是變數,分母不為零,代碼區為L。

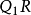

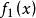
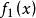
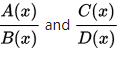

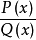
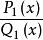
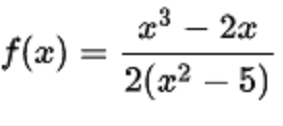
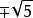
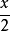


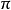

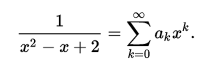
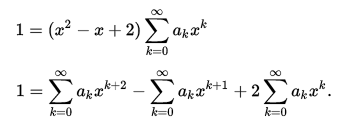


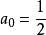
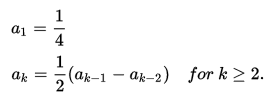

有理函式是通過多項式的加減乘除得到的函式。在數學中,理性函式是可以由有理分數定義的任何函式,即代數分數,使得分子和分母都是多項式。 多項式的係數不需要是有理...
有理函式積分法是按一定步驟求有理函式不定積分的方法,求有理函式的積分時,先將有理式分解為多項式與部分分式之和,再對所得到的分解式逐項積分。有理函式的原...
矩陣中的元素為有理函式的矩陣稱為有理函式矩陣。而有理函式的定義為:通過多項式加減乘除得到的函式稱為有理函式,可以寫成如下形式: h=f/g 這裡f和g都是...
無理函式是一種代數函式,不是有理函式的代數函式稱為無理函式,或者說對應規律含對自變數的開方運算的代數函式稱為無理函式,無理函式通常是自變數包含在根式(通常...
trigonometric function)與常數經過有限次的有理運算(加、減、乘、除、有理數次乘方、有理數次開方)及有限次函式複合所產生,並且能用一個解析式表示的函式。它...
有理分式指的是兩個多項式的商,又稱為有理函式,具體來說是指分子及分母都是多項式的分式。...
有理正實函式(rational positive real function)一類復變數有理函式...... 有理正實函式(rational positive real function)一類復變數有理函式.有理正實函式(rationa...
系統函式是個具有實係數的復變數S的有理函式,即實有理函式,所以它的極點和零點或者是實數而位於實軸上,或者是成共軛對的複數而位於與實軸對稱的位量上。就是...
而有理簇(rational variety)是雙有理等價於代數閉域上的射影空間的代數簇。它當然是最簡單的代數簇。它可以等價地定義為代數閉域k上的代數簇X,X的有理函式域...
《復變函式論》俄文原為俄羅斯師範學院數學系的教學參考書,《復變函式論》在內容安排上與傳統的教材有很大的不同,《復變函式論》共分為九章,作者從復變函式論...
初等函式(有理函式、指數函式、三角函式與雙曲函式、根式函式、對數函式、一般冪函式與一般指數函式、反三角函式與反雙曲函式等)、解析函式的基本特徵、解析函式的...
ζ 函式(ζ-function)是用來刻畫系統周期點性態的函式,是動力微分系統的重要研究對象。Smale猜測公理A微分同胚有有理的ζ函式,以後Maninng使用Markov分解這一手段...
《多元有理函式系統與電網路》鑒於實數域上線性系統和電網路描述不便於研究系統和電網路的結構性質的問題,《多元有理函式系統與電網路》提出用多元有理函式域F(z)...
如果支持向量機的求解只用到內積運算,而在低維輸入空間又存在某個函式 K(x, x′) ,它恰好等於在高維空間中這個內積,即K( x, x′) =<φ( x) ⋅φ( ...
有理函式是兩個代數多項式之比,其中分母在所考慮的自變數區間內不等於零。在切比雪夫研究多項式逼近的同時也就已經考慮了有理函式的最佳逼近理論。但真正受到重視是...
部分分式分解(partial fraction decomposition) 亞純函式在極點處的一種表示式。部分分式分解或部分分式展開,是將有理函式分解成許多次數較低有理函式和的形式,來...
[5]沈燮昌 具有給定極點的有理函式的逼近與展開(一)[J]數學研究與評論1982年(02)[6]沈燮昌 E~1類中多項式和有理函式的最佳逼近[J]數學研究與評論1982年(03...
