有理函式域(rational function field)是一種重要的純超越擴張。純超越擴張是一類重要的超越擴張。設擴域K在F上的超越基為S,若K=F(S),則稱此域擴張為純超越擴張,K為F的純超越擴域。
基本介紹
- 中文名:有理函式域
- 外文名:rational function field
- 領域:數學
- 學科:域論
- 性質:一種重要的純超越擴張
- 上層概念:超越擴張
概念
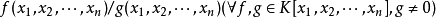
有理函式域(rational function field)是一種重要的純超越擴張。純超越擴張是一類重要的超越擴張。設擴域K在F上的超越基為S,若K=F(S),則稱此域擴張為純超越擴張,K為F的純超越擴域。
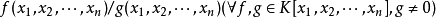
有理函式域(rational function field)是一種重要的純超越擴張。純超越擴張是一類重要的超越擴張。設擴域K在F上的超越基為S,若K=F(S),則稱此域擴張為純超越...
有理函式是通過多項式的加減乘除得到的函式。在數學中,理性函式是可以由有理分數定義的任何函式,即代數分數,使得分子和分母都是多項式。 多項式的係數不需要是有理...
二次代數函式域,明顯決定了幾類實二次函式域的基本單位,決定了多類二次函式域的理想類數的下界,給出了類數為 1 的條件,給出了理想類群的結構的一系列定理。...
有理映射是代數簇上的有理函式概念的推廣。但是,它並不是集合意義下的映射。代數簇是代數幾何的基本研究對象。設k是一個域,域k上的代數簇就是一個整的、分離...
《多元有理函式系統與電網路》鑒於實數域上線性系統和電網路描述不便於研究系統和電網路的結構性質的問題,《多元有理函式系統與電網路》提出用多元有理函式域F(z)...
而有理簇(rational variety)是雙有理等價於代數閉域上的射影空間的代數簇。它當然是最簡單的代數簇。它可以等價地定義為代數閉域k上的代數簇X,X的有理函式域...
亞純函式是在區域D上有定義,且除去極點之外處處解析的函式。在複分析中,一個複平面的開子集D上的亞純函式是一個在D上除一個或若干個孤立點集合之外的區域全...
trigonometric function)與常數經過有限次的有理運算(加、減、乘、除、有理數次乘方、有理數次開方)及有限次函式複合所產生,並且能用一個解析式表示的函式。它...
半純函式是一種復變函式,即自變數和因變數都取值複數, 也稱亞純函式。半純函式是在區域D上有定義,且除去極點之外處處解析的函式。在複分析中,一個複平面的開子...
域,數學辭彙,定義域,值域,數學名詞,函式經典定義中,因變數改變而改變的取值範圍叫做這個函式的值域,在函式現代定義中是指定義域中所有元素在某個對應法則下對應的...
域的特徵是交換代數中的基本概念。 一個域就是滿足加、減、乘、除 四則運算的集合。 比如有理數域, 有理函式域, 代數數域、伽羅華域等等。...
若一個代數簇V1到另一個代數簇V2的映射誘導了函式域之間的同構,則稱該映射為雙有理映射。設有兩個代數簇V1,V2,若V1中有一個稠密開集同構於V2的一個稠密...
他深入研究了一個方程能用根式求解所必須滿足的本質條件,他提出的“Galois域”...還解決了有理函式域的有限有理基的存在問題。對有限群的不變式具有有限基給出...
曾炯之,即曾炯(1897—1940),數學家。我國最早從事抽象代數研究的學者,在有關函式域上代數的研究中獲得重要成果。...
還解決了有理函式域的有限有理基的存在問題。對有限群的不變式具有有限基給出一個構造性證明。她不用消去法而用直接微分法生成微分不變式,在哥廷根大學的就職...
超橢圓曲線的函式域(超橢圓函式域)是有理函式域的二次擴張;從這個意義上講它是除了有理函式域之外的最簡單的代數函式域。虧格為2的曲線必定是超橢圓曲線。 超...
曾炯,即曾炯之,數學家。中國最早從事抽象代數研究的學者,在有關函式域上代數的研究中獲得重要成果。...
伽羅瓦群為可交換群的數域,阿廷互反律向這個伽羅瓦群的任何一支一維表示配上一枚L函式,並斷言:此等 L-函式俱等於某些狄利克雷L函式(黎曼ζ函式的類推,由狄利克...
創立了有理函式域論,引進了在域上添加代數量生成擴域的概念和模系的概念,因而使代數數的理論獨立於代數基本定理;發現有理數域的任一阿貝爾擴張一定是一分圓域的...
