基本介紹
- 中文名:超橢圓曲線
- 外文名:hyperelliptic curve
- 基本形式:y^2+h(x)y=f(y)
- 套用:超橢圓曲線密碼
簡介
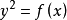

判定




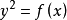




設C是代數曲線,如果存在一個從C到射影直線P¹的二次覆蓋(即全純的2:1滿射),就稱C是超橢圓曲線。超橢圓曲線在密碼學中有很大的套用。美國華盛頓大學教授Neal...
g>2 的曲線中存在非超橢圓曲線。 [3] 代數曲線研究方法 編輯 代數曲線模空間觀點 具有同樣虧格的曲線的等價類組成的集合稱為曲線模空間。 比如...
橢圓曲線加密法(ECC)是一種公鑰加密技術,以橢圓曲線理論為基礎,在創建密鑰時可做到更快、更小,並且更有效。ECC 利用橢圓曲線等式的性質來產生密鑰,而不是採用傳統...
設X是代數曲面, B是代數曲線。 f:X→B是曲面纖維化。 如果幾乎所有的纖維 F 都是超橢圓曲線, 那就稱 f:X→B 是超橢圓纖維化。 肖剛、Horikawa 等人在超...
我們也可以看到為什麼g=2 的情形是特殊的,由超橢圓曲線理論,其序列開始幾項為1, 1, 2, ...這些結論為何具有這種形式可以追溯到此定理的表述(羅赫的部分):兩...
《算法數論》是2002年科學出版社出版的圖書,作者是裴定一。本書論述了算法數論的基本內容,其中包括連分數、代數數域、橢圓曲線、素性檢驗、大整數因子分解算法、橢圓...
基於格的公鑰體制和橢圓曲線及超橢圓曲線密碼體制等; 第6章較全面地介紹了數字簽名的思想及方法,包括幾種經典的數字簽名算法和體制以及國內外在簽密方面的最新研究...
·橢圓曲線與超橢圓曲線密碼設計與分析·密鑰共享理論技術研究·安全多方計算·代數攻擊·數字簽名(b) 技術研發:·具有身份認證的二維條碼理論與技術(與軟體所合作)...
方躍堅,沈晴霓,吳中海,一種超橢圓曲線密碼處理器並行結構設計,計算機研究與發展, 2013,50(11):2383-2388。Yuejian Fang, Zhonghai Wu, Xiaohui Duan, Jianqiang ...
164 利用有效的求逆算法快速計算超橢圓曲線標量乘 郝艷華; 姜正濤; 王育民 【期刊】西安電子科技大學學報 2005-06-20165 基於有限域的最佳周期交織方法 王瑩; ...
21.郝艷華,姜正濤,王育民.利用有效的求逆算法快速計算超橢圓曲線標量乘.西安電子科技大學學報, 2005, Vol. 32, No. 3, 418-422....
6.3.5 基於超橢圓曲線密碼體制的密碼協定 6.4 基於身份的公鑰密碼體制 6.4.1 基於身份的密碼體制簡介 6.4.2 BF方案及其安全性 參考文獻 第七章 字簽名與...
1、2006年出版專著《超橢圓曲線密碼體制的理論與實現》(獨著),經濟管理出版社;2、2015年出版專著《虛擬計算環境的運行時資源監控與內在泄漏檢測技術》獨著,電子工業...
馮君,汪學明.基於超橢圓曲線密碼體制的RFID安全協定.計算機工程與設計(核心期刊),2013年11月第11期(已錄用)。 湯玉,汪學明.一種分層路由協定的改進和仿真分析. ...
橢圓與超橢圓曲線公鑰密碼的理論與實現 王學理(1) 科學出版社,2006 組合矩陣論(第二版) 柳柏濂 科學出版社,2005 點集拓撲講義(第三版) 熊金城 高等教育出版...
現工作於電子科技大學計算機科學與工程學院。廖永建博士的研究領域主要為安全可證明的密碼算法、橢圓曲線與超橢圓曲線理論等等。科研情況...
46.付治國, 術洪亮, 張樹功, 虧格為3的超橢圓曲線除子類群的計算公式, 吉林大學學報(理學版) 2009, 47(02) 201-206.47.王禮萍 張樹功, 重言式和矛盾式的...
後,本書以一半的篇幅詳細介紹了安全通信所涉及的公鑰密碼學新成果,包括橢圓曲線密碼、超橢圓曲線密碼、雙線性對密碼、格密碼等,並簡要介紹了安全與鑑別密碼協定。本...
