基本介紹
簡介
拓撲
定向表面


舉例
 genus 0
genus 0 genus 1
genus 1 genus 2
genus 2 genus 3
genus 3不定向表面
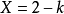
結
柄體

圖論
代數幾何
相關例子
 虧格
虧格 虧格
虧格 虧格
虧格


 genus 0
genus 0 genus 1
genus 1 genus 2
genus 2 genus 3
genus 3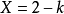

 虧格
虧格 虧格
虧格 虧格
虧格虧格是代數幾何和代數拓撲中最基本的概念之一。定義:若曲面中最多可畫出n條閉合曲線同時不將曲面分開,則稱該曲面虧格為n。以實的閉曲面為例,虧格g就是曲面上...
最大虧格(maximum genus)是圖的一個組合不變數。圖G所能嵌入而形成地圖的曲面中,具有最大虧格的(不)可定向曲面的虧格稱為圖G的(不)可定向的最大虧格。圖G所...
幾何虧格(geometric genus)與標準叢相關的復維數.設M為m維緊複流形,K(M)表示M的標準叢nmT~ cM>. M的幾何虧格P} (M)為 dimcC}(lCK(M))). ...
橢圓曲線是域上虧格為1的光滑射影曲線。對於特徵不等於2的域,它的仿射方程可以寫成:y^2=x^3+ax^2+bx+c。複數域上的橢圓曲線為虧格為1的黎曼面。Mordell...
若一個閉曲面(或開曲面)上的一維同調群(或模理想邊界的一維同調群)的秩是2g,則稱g (非負整數或無窮)為此黎曼曲面的虧格。開曲面的虧格可能為無窮。兩個黎曼...
從而代數曲線的最重要的數值不變數——虧格也可用各種不同的方式來定義:它既是一個拓撲不變數,也是一個可由緊黎曼面上的整體全純微分形式空間的維數或以結構層...
1987~1990年,肖剛建立一個關於纖維化斜率的不等式λ≥4(g-1)/g證明某一類低斜率一般型曲面中一定存在虧格較低的纖維化;得到了纖維化的不規則性的上界的幾個...
這樣得到的地圖M′稱為M的對偶地圖,這裡的對偶性也是對稱的,即,若M′為M的對偶地圖,則M也為M′的對偶地圖,若(不)可定向地圖M對於任何虧格小於M的虧格的(不...
按其最初形式,這個猜想是說,任一不可約、有理係數的二元多項式,當它的“虧格”大於或等於2時,最多只有有限個解。記這個多項式為f(x,y),猜想便表示:最多...
七色定理是指在虧格為一的環面上染色需要七種不同顏色。...... 七色定理是指在虧格為一的環面上染色需要七種不同顏色。中文名 七色定理 外文名 Seven color ...
黃元秋,男,教授,博士生導師,1966年出生,湖南師範大學數學系主任,湖南省數學學會常務理事。主要從事拓撲圖論中的圖的最大虧格及其上可嵌入性、圖的下可嵌入性、圖...
證明:虧格為零的常平均曲率閉曲面必是球面.他於195。年提出以下猜想:R3中常平均曲率的緊緻閉曲面必是球面.這個問題直至1985年懷特(Wente,H.C.)構造出了R3中...
洞的個數在數學上稱為曲面的虧格原始的Enneper曲面是一個著名的極小曲面,也就是說它上面任何一條小封閉曲線圍成的曲面的面積總是最小的,即任何以這條曲線為...
