基本介紹
- 中文名:閉曲面
- 外文名:Closed surfaces
- 涵義:緊湊且沒有邊界的表面
- 分類:可定向曲面與不可定向曲面
- 示例:球體、環面、克萊恩瓶子
- 相關名詞:開曲面
簡介
分類


單結構
邊界表面

黎曼表面
非緊湊表面
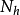

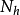





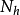

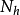

閉曲面是指沒有邊界點的緊緻連通2維實流形(曲面)。它分為可定向曲面與不可定向曲面。封閉的表面是緊湊且沒有邊界的表面。 示例是像球體,環面和克萊恩瓶子這樣...
在數學中,黎曼曲面是德國數學家黎曼為了給多值解析函式構想一個單值的定義域而提出的一種曲面。用現代的語言說,黎曼曲面就是連通的一維複流形。黎曼曲面的研究...
克萊茵曲面是由德國數學家克萊茵首先研究的,又稱克萊茵壺或克萊茵瓶,是一種單側曲面,克萊茵曲面亦是拓撲學的基本圖形之一。把兩個莫比烏斯帶沿著邊界黏合起來便...
它給出了閉曲面積分和相應體積分的積分變換關係,是矢量分析中的重要恆等式,也是研究場的重要公式之一。 物理套用 矢量分析 高斯定理是矢量分析的重要定理之一。...
霍普夫猜想是關於常平均曲率曲面的一個猜想,即具有常平均曲率的凸閉曲面必是球面(參見“球面的剛性”)。...
環面(torus)是一個麵包圈形狀的旋轉曲面,由一個圓繞一個和該圓共面的一個軸迴轉所生成。在拓撲學上,環面是一個定義為兩個圓的積的閉合曲面。...
高斯面是高斯定理中的任一閉合曲面,指真空中的任何靜電場中,穿過任一閉合曲面的電通量,在數值上等於該閉合曲面內包圍的電量的代數和乘以1/ε。...
更詳細地說,這定律描述穿過任意閉曲面的電通量與這閉曲面內的電荷之間的關係。 高斯磁定律:該定律表明,磁單極子實際上並不存在。所以,沒有孤立磁荷,磁場線沒有...
通過任意閉合曲面的磁通量 ΦB 等於通過構成它的那些面元的磁通量的代數和,即對於閉合曲面,通常取它的外法線矢量(指向外部空間)為正。 在一般情況下,磁通量是...
在電磁學中,電通量(符號:ΦE)是電場的通量,與穿過一個曲面的電場線的數目成正比,是表征電場分布情況的物理量。...
虧格是代數幾何和代數拓撲中最基本的概念之一。定義:若曲面中最多可畫出n條閉合曲線同時不將曲面分開,則稱該曲面虧格為n。以實的閉曲面為例,虧格g就是曲面上...
非迴轉面在工程實踐中,常用的非迴轉面是由直母線運動面形成的直紋曲面,直紋曲面分為:(1)可展直紋曲面一一曲面上相鄰兩素線是相交或平行的共面直線,這種曲面...
佩克索托定理(Peixoto's theorem)定向閉曲面上C向量場X結構穩定的特徵性定理.該定理指出:X是C'<r>1)結構穩定的充分必要條件是X是莫爾斯一斯梅爾系統.具體地,...
卵形面是一類有顯明幾何特徵的緊緻閉曲面,高斯曲率處處為正的曲面稱為凸曲面,緊緻的凸閉曲面稱為卵形面。對於卵形面有著名的阿達馬定理,因此,卵形面微分同胚於...
