基本介紹
定義
相關概念
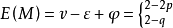
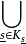
分類
 圖1
圖1 圖2
圖2 圖3
圖3 圖4
圖4 圖4
圖4 圖5
圖5 圖6
圖6
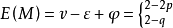
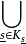
 圖1
圖1 圖2
圖2 圖3
圖3 圖4
圖4 圖4
圖4 圖5
圖5 圖6
圖6三角剖分是代數拓撲學裡最基本的研究方法。 以曲面為例, 我們把曲面剖開成一塊塊碎片,要求滿足下麵條件: (1)每塊碎片都是曲邊三角形; (2)曲面上任何兩個這樣...
點集的三角剖分(Triangulation),對數值分析(比如有限元分析)以及圖形學來說,都是極為重要的一項預處理技術。尤其是Delaunay三角剖分,由於其獨特性,關於點集的很多...
三角剖分公式 20世紀初,數學家烏拉班發現並證明了下面的公式,(Dn表示凸n邊形的三角剖分數).D(n+1)/Dn=(4n-6)/n. 1.問題之假設 所得三角形必須以原凸...
單純剖分(simplicial subdivision)是一種組合構形。它是對於平面上三角形所做的一種三角剖分。若在這個三角剖分中,任何兩個三角形的公共部分不是點就是其中一個...
《Delaunay三角剖分理論及可視化套用研究》是2010年哈爾濱工業大學出版社出版的圖書,作者是李海生。...
等積三角剖分猜想:將一個正方形(猜想之中的正方形可以換成長方形)分割成若干個面積相同的三角形(形狀未必相同),那么三角形個數必為偶數。此猜想屬於組合和拓撲...
Delaunay三角化是一種三角剖分DT(P),使得在P中沒有點嚴格處於DT(P)中任意一個三角形外接圓的內部。Delaunay三角化最大化了此三角剖分中三角形的最小角,換句...
1 名稱 2 畫法 3 日常套用 4 三角剖分 曲邊三角形名稱 編輯 curved edge triangle,又稱魯洛三角形Reuleaux triangle。 曲邊三角形 曲...
3 直角球面三角形 ▪ 簡介 ▪ 納皮爾法則 4 基於等角比例投影的球面三角四叉樹剖分模型 ▪ 研究進展 ▪ 剖分模型的幾何性質比較 ▪ 研究結論...
●「ドロネー三角形分割/Delaunay Triangulation(德勞內三角化)」:在數學和計算幾何領域,平面上的點集「P」的「德勞內三角化」是一種「三角剖分DT(P)」,使得在...
單純形剖分( simplicial partition, simplicial subdiviSion)亦稱“三角剖分”( triangulation)。 ...
三角地圖(triangulation)亦稱三角剖分一類特殊的圖.它是所有面都是三角形(面邊界是長度為3的圈)的地圖.若在一個二角地圖所相應的圖中沒有重邊,則稱它為嚴格...
Voronoi圖是Delaunay三角剖分的對偶圖,生成它的方法有很多 [3] ,比較有名的有分治算法,掃描線算法,增量法等。但利用Delaunay三角剖分生成Voronoi圖的算法是最快的...
對散亂點進行三角剖分的方法很多,其最佳化準則有五,即Thiessen區域準則、最小內角最大準則、圓準則、ABN準則及PLC準則。(1) Thiessen區域準則(Thiessen regioncriterion...
全書共分11章,包括:預備知識,幾何查找(檢索),多邊形,凸殼及其套用,Voronoi圖、三角剖分及其套用,交與並及其套用,多邊形的獲取及相關問題,幾何體的劃分與等分、算法...
