Voronoi圖是一組連續多邊形組成,多邊形的邊界是由連線的垂直平分線組成。M 個在工平面上有區則的點。按照最近鄰原則劃分平面,每一個點與它最近鄰的區域關聯,與每個點相關聯的區城(成多邊用是唯一的,它由這些點的空網分布所決定。
基本介紹
- 中文名:voronoi圖
- 外文名:Voronoi diagram
- 所屬領域:計算幾何
- 提出者:喬奇·沃若諾依(Georgy Voronoi)
- 其它名稱:Voronoi劃分,Voronoi鋪砌
幾何定義

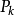

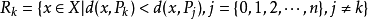

Voronoi圖是一組連續多邊形組成,多邊形的邊界是由連線的垂直平分線組成。M 個在工平面上有區則的點。按照最近鄰原則劃分平面,每一個點與它最近鄰的區域關聯,與每個點相關聯的區城(成多邊用是唯一的,它由這些點的空網分布所決定。

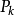

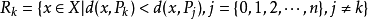
Voronoi圖是一組連續多邊形組成,多邊形的邊界是由連線的垂直平分線組成。M 個在工平面上有區則的點。按照最近鄰原則劃分平面,每一個點與它最近鄰的區域關聯,與...
《Voronoi圖及其套用》是2013年9月26日出版的圖書,作者是楊承磊、呂琳、楊義軍、孟祥旭等。...
《基於Voronoi圖的GIS空間關係計算》是2006年中國測繪出版社出版的圖書,作者是趙仁亮。...
Voronoi圖,又叫泰森多邊形或Dirichlet圖,它是由一組由連線兩鄰點直線的垂直平分線組成的連續多邊形組成。N個在平面上有區別的點,按照最鄰近原則劃分平面;每個點與...
《限定Voronoi格線剖分的理論及套用研究》是2010年北京郵電大學出版社出版的圖書,作者是蔡強。...
如圖,其中虛線構成的多邊形就是泰森多邊形。泰森多邊形每個頂點是每個三角形的外接圓圓心。泰森多邊形也稱為Voronoi圖,或dirichlet圖。中文名 泰森多邊形法 類別 氣象...
17.閆浩文、郭仁忠,測繪科學,2002年3月,Volo.27 No.1,基於Voronoi圖的空間方向關係形式化描述模型研究(一),ISSN 1009-2307,CN 11-4415/p...
2. [宗大偉. Voronoi圖及其套用研究[D].南京航空航天大學,2006. 3. 石朝俠,洪炳鎔,周彤,王燕清. 大規模環境下的拓撲地圖創建與導航[J]. 機器人,2007,(05)...
1)楊承磊,呂琳,楊義軍,孟祥旭,Voronoi圖及其套用。清華大學出版社,20132)汪嘉業,王文平,屠長河,楊承磊。計算幾何及套用。科學出版社,2011...
系統將計算幾何原理套用到空間數據處理中的複雜算法運算,基於Delaunay三角網,Voronoi圖,凸殼和矩形幾何的原理模型,設計完成了地圖綜合中的化簡,合併,移位,骨架化等操作...
