二次代數函式域,明顯決定了幾類實二次函式域的基本單位,決定了多類二次函式域的理想類數的下界,給出了類數為 1 的條件,給出了理想類群的結構的一系列定理。發展套用了函式連分式理論。
基本介紹
- 中文名:代數函式域
- 外文名:Algebraic function field
- 套用學科:數學
- 適用領域範圍:有理函式
概念
性質
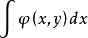
域的擴張
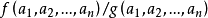
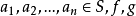
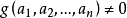

二次代數函式域,明顯決定了幾類實二次函式域的基本單位,決定了多類二次函式域的理想類數的下界,給出了類數為 1 的條件,給出了理想類群的結構的一系列定理。發展套用了函式連分式理論。
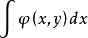
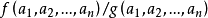
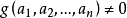
二次代數函式域,明顯決定了幾類實二次函式域的基本單位,決定了多類二次函式域的理想類數的下界,給出了類數為 1 的條件,給出了理想類群的結構的一系列定理。...
求有理函式的反函式則可產生代數函式。如y=xn的反函式為x=yn。 [2] 初等函式超越函式 超越函式指變數之間的關係不能用有限次加、減、乘、除、乘方、開方運算...
《函式域中的數論》是2011年世界圖書出版公司出版的圖書,作者是(美)羅森。... 本書在介紹完函式域上的基本資料以後,接下來深入剖析全局函式域和代數數域之間的...
值域,數學名詞,在函式經典定義中,因變數改變而改變的取值範圍叫做這個函式的值域,在函式現代定義中是指定義域中所有元素在某個對應法則下對應的所有的象所組成的...
《近世代數講義》根據作者在復旦大學多年教學的講義修改而成,內容包括群的基本知識、環和域的基本知識、多項式和有理函式、向量空間、群論中一些進一步的知識、域的...
函式環是定義在集合 L 上,取值於某數域 K 中的全體(具有某種給定性質的)函式的集合 KL ,關於函式的加法、乘法運算做成的環,稱為定義在 L 上的(具有某種性質...
1 簡介 2 在歐幾里得幾何中 3 非平面代數曲線 4 代數函式域 5 理性曲線 五次曲線簡介 編輯 在數學中,平面實數代數曲線是歐幾里得平面上的坐標集合,其坐標是...
在數學中,黎曼曲面是德國數學家黎曼為了給多值解析函式構想一個單值的定義域而提出的一種曲面。用現代的語言說,黎曼曲面就是連通的一維複流形。黎曼曲面的研究...
的實數理論、求解數列極限的若干典型求法、函式的極限與連續性、微分和積分中值定理、數項級數、函式項級數、不等式、變分法、函式的逼近與開拓以及代數中的分析...
設是定義在數域 k 上的函式, 我們把方程 f=0 在數域 k 中的解稱作f (在k中)的零點. 所有零點構成的集合稱作零點集。...
