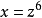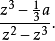有理分式指的是兩個多項式的商,又稱為有理函式,具體來說是指分子及分母都是多項式的分式。
基本介紹
- 中文名:有理分式
- 外文名:rational fraction
- 拼音:yǒu lǐ fēn shì
- 專業:數學
有理分數的背景術語,有理分式的代數表達,區別於有理分式的無理分式,
有理分數的背景術語
在代數分式 中,被除數稱為分子,除數稱為分母,兩者都是代數分式的項。
中,被除數稱為分子,除數稱為分母,兩者都是代數分式的項。

若代數分式的分子或分母中包括複數,則稱為複數分式。
簡分式是其分子或分母都不是分式的代數分式,若一個表示式不是以分式的形式表示,則稱為整式,不過只要將分母設為1,即可以將整式表示為代數分式,帶分式指整式和分式的代數和。
有理分式的代數表達
若代理分式的a和b都是多項式,此分式稱為有理代數分式,或簡稱為有理分式。有理分式也稱為有理表示式或有理函式。若有理分式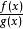 滿足
滿足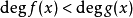 ,稱為真分式,否則稱為假分式,像
,稱為真分式,否則稱為假分式,像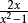 為真分式,而
為真分式,而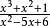 和
和 是假分式。假分式可以表示為整式(可能是常數)及真分式的和,例如以上提到的假分式可以表示為
是假分式。假分式可以表示為整式(可能是常數)及真分式的和,例如以上提到的假分式可以表示為
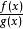
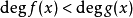
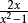
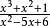

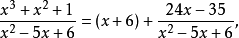
其中第二項為真有理分式,二個真分式的和也會是真分式,有時會將真分式的分母因式分解,再將真分式表示數個真因式,其分母分別為原分母的因式(或因式次方),這稱為部分分式,例如以下等號右邊的即為部分分式
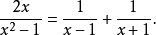
區別於有理分式的無理分式
無理分式是指分式中有變數的冪式為小數,像以下的分式即為無理分式
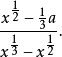
將無理分式變為有理分式的過程稱為有理化,每個根式為單項的無理分式可以用以下的方式有理化:找到所有冪次分母的最低公倍數,再將變數用另一變數的冪次取代,使原來的根式都變為新變數的整數冪次,例如在上式中,冪次分母的最低公倍數為6,因此可以令 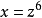 ,得到
,得到