分式方程和整式方程統稱有理方程。其中分式方程是分母含未知數的方程,整式方程是等號兩邊都為整式的方程。
基本介紹
- 中文名:有理方程
- 外文名:rational function
表達式,解法,整式方程,分式方程,
表達式
有理方程的表達式可寫為F(x)=P(x)/Q(x),P(x)與Q(x)皆為多項式方程。Q(x)不等於0或1。
解法
整式方程
依據:等式的性質1 等式兩邊加或減同一個數或式子,結果仍相等。
等式的性質2 等式兩邊乘同一個數,或除以同一個不為0的數,結果仍相等。
例題:1.解一元一次方程:-0.5x+7=9.
解:移項(把等式一邊的某項變號後移到另一邊),得-0.5x=9-7.
合併同類項,得-0.5x=2.
係數化為1,得x=-4.
2.解一元二次方程:x2+5x=6.
解法一:移項,得x2+5x-6=0.
因式分解,得(x+6)(x-1)=0.
於是,得x+6=0,或x-1=0,
x1=-6,x2=1.
解法二:配方,得x2+5x+2.52=6+2.52,
(x+2.5)2=12.25.
由此可得x+2.5=±3.5,
x1=-6,x2=1.
解法三:化為一般形式x2+5x-6=0.
a=1,b=5,c=-6.
△=b2-4ac=52-4×1×(-6)=49>0.
方程有兩個不等的實數根
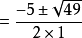
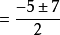 ,
,

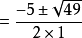
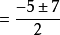
即x1=-6,x2=1.
分式方程
方法:兩邊乘最簡公分母化分式方程為整式方程,得出解後驗根。
例題:解方程: .
.

解:方程兩邊乘(x-9)(x-5),得x(x-5)-36=2(x-9).
解得x1=9,x2=-2.
檢驗:當x=9時,(x-9)(x-5)=0.
當x=-2時,(x-9)(x-5)≠0.
所以原方程的解是x=-2.
