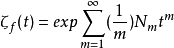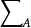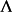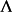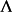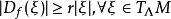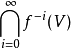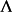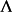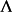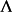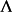ζ函式

ζ 函式(ζ-function)是用來刻畫系統周期點性態的函式，是動力微分系統的重要研究對象。

Smale猜測公理A微分同胚有有理的ζ函式，以後Maninng使用Markov分解這一手段得出證明。張築生證明了擴張自映射有有理的ζ函式。馮慶富通過公理A*的使用，證明了：①公理A自覆蓋映射具有“Markov分解”，這是公理A微分同胚相應結果的推廣；②公理A自覆蓋映射有有理的ζ函式。

基本介紹

• 中文名：ζ函式
• 外文名：ζ-function
• 定義：刻畫系統周期點性態的函式
• 學科：數學
• 領域：微分動力系統

定義

ζ 函式(ζ-function)是用來刻畫系統周期點性態的函式。設M是微分流形，f：M→M是可微映射，對m=1,2,...，記N_m=N_m(f)為f^m的不動點數目。假設N_m<+∞，m=1,2, ...，如下形式的冪級數：

稱為f的ζ函式。ζ函式最早由阿廷(Artin，E.)和馬祖爾(Mazur，B.)於1965年給出。它是一個共扼不變數，因而可記ζ_f(t)為ζ(t)。在什麼條件下ζ(t)是有理函式是動力系統研究的重要問題。現已證明：公理A微分同胚以及擴張映射的ζ函式是有理的。對M上可微流φ的ζ函式是由斯梅爾(Smale，S.)給出的，其形式為無窮積：。

這裡Γ是φ的除奇點外的周期軌道的集合，ζ(γ)是周期軌道的周期。

記號定義

定義1

設X是拓撲空間，f：X→X是連續映射，fⁿ的不動點數N_n(f)<+∞，任意n∈N，則稱

為f的ζ函式。

定義2

以 表示形狀如 的序列的集合，這裡a_i取值於{1,2,…,h}。 中的距離定義為。

這裡 ， ，

又以σ表示轉移映射：

設A=(A(j,k))是h*h方陣，其中各A(j,k)是0或1。我們把 （或 ）稱為是A允許序列，如果

所有形狀如 的A允許序列組成的 的子集記為 ， 稱為有限型子轉移。

定義3

設M是微分流形，U M是具有緊緻閉包的開集，A U是緊緻集，f∈C¹(U,M)，f( ) 。f稱為是在 上擴張的，如果存在M的Riemann度量<·,·>和實數r>1使得

。

這裡|·|表示由<·,·>引出的範數。特別地，如果M是緊緻的，f∈C¹(M,M)在M上擴張，則稱f是擴張映射。

定義4

f∈C⁰(U,M)稱為在 中正向可擴，如果 ，並且存在（被稱為可擴常數的）e>0使得對任意x,y∈ ，x≠v，存在非負整數k滿足d(f^k(x),f^k(y))>e。

如果f∈C¹(U,M)在緊緻不變集 U上擴張，則存在 的緊鄰域V U使得f在V中是正向可擴的。

集合S的基數記為#S。

定理及引理

定理1

緊緻光滑流形M上的擴張自映射f具有有理的ζ函式。

定理2

設M是光滑流形，f∈C¹(M,M)， 是緊緻集，f在上是擴張的，則ζ_f(t)是有理函式。

引理1

設f∈C¹(M,M)在緊緻集=上是擴張的，<·,·>和r如定義3所述。則存在緊鄰域V和實數1<r'<r，ρ>0，使得：對任意x∈V映射f|B(x,ρ)是到象集的微分同胚，對任意p,q∈B(x,ρ)，f(p),f(q)∈B(f(x),r’ρ)有d(f(p),f(q))≥r’d(p,q)。

並且對任意x∈V，0<ρ'<ρ有f(B(x,p'))B(f(x),r'ρ')。

引理2

設W∈int V是=的緊鄰域，則對任意β>0，存在0<α<β，使得W中的任意α偽軌有V中的軌道β追蹤它。

設e是f在V中的可擴常數。選取β滿足，選取α滿足0<α<β min{r-1,1}，再選取δ,0<δ<α/2，使得對於任意x,y∈V，d(x,y)<δ，有d(f(x),f(y))<α/2。記

選取p₁,...,p_s∈W使得

以P_i表示滿足以下條件的點y∈Δ的集合：從y出發的軌道可以β追蹤形狀如{p_i,p_α1,p_α2,...}的α偽軌。又以p_i'表示P_i在子空間Δ中的內點集。

引理3

=。

公理A

公理A是在微分動力系統結構穩定性和Ω穩定性的研究中，由斯梅爾提出的一個基本條件。滿足公理A條件要求的系統被稱為公理A系統。設M是緊緻微分流形，f：M→M是微分同胚。涉及f的以下條件稱為公理A系統：

1.非遊蕩集Ω(f)具有雙曲結構；

2.周期點在非遊蕩集中稠密；

對M上的C向量場X來說，設φ是X導出的流，若Ω(φ)=F∪ ，同時滿足：

1.F是φ的有限個雙曲奇點的集合；

2. 是φ的雙曲不變集，而且φ的雙曲周期軌在 中稠；

3.F∩ =φ；

則稱φ為公理A流。

莫爾斯-斯梅爾系統以及安諾索夫系統都是公理A系統。斯梅爾正是在概括了這兩個系統及其他結構穩定系統後提出公理A條件的。公理A系統的遍歷性質及其非遊蕩集的結構等動力學性質的研究已取得豐富成果。