雙伽瑪函式是伽瑪函式的對數導數。
基本介紹
- 中文名:雙伽瑪函式
- 外文名:Digamma function
- 分類:數理科學
第一個多伽瑪函式
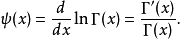
與調和數的關係
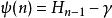
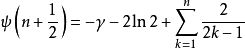
積分表示法
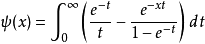

泰勒級數
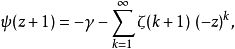
牛頓級數

反射公式
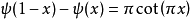
遞推關係

高斯和

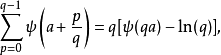
高斯雙伽瑪定理

特殊值
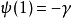

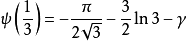
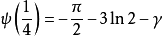
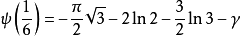
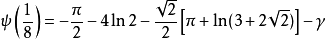
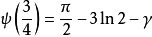
參見
- 三伽瑪函式
- 多伽瑪函式
雙伽瑪函式是伽瑪函式的對數導數。
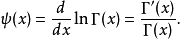
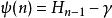
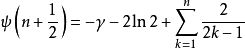
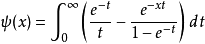

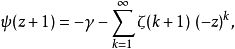

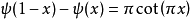


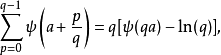

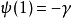

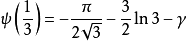
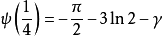
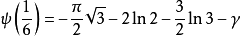
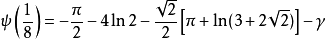
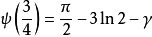
雙伽瑪函式是伽瑪函式的對數導數。...... 雙伽瑪函式與調和數的關係 編輯 雙伽瑪函式,通常用ψ0(x)、ψ(x)或 F來表示,與調和數有以下的關係:...
特殊函式是指一些具有特定性質的函式,一般有約定俗成的名稱和記號,例如伽瑪函式、貝塞爾函式、菲涅耳積分等。它們在數學分析、泛函分析、物理研究、工程套用中有著舉足...
階乘的定義可推廣到複數,其與伽瑪函式的關係為:伽瑪函式滿足 。階乘函式遞進/遞降階乘 遞進階乘:遞降階乘:階乘函式雙階 表示雙階乘,其定義為:...
伽瑪分布是統計學中的一種連續機率函式,包含兩個參數α和β,其中α稱為形狀參數,β稱為尺度參數。...
當把雙階乘的定義域擴展到實數域的時候,雙階乘的值改變了,如[1]: 其中(x/2)!的定義參見伽瑪函式。 在此定義下,奇數的雙階乘值沒有改變,而偶數的雙階乘值在...
(Beta Distribution) 是一個作為伯努利分布和二項式分布的共軛先驗分布的密度函式,...其中 表示雙伽瑪函式。8. 聯合熵為:9.KL散度其為:貝塔分布實例 編輯 ...
Ϝ代表: 有時用作表示雙伽瑪函式,但通常被拉丁字母 F(差不多一樣)替代。希臘字母Ζζ ζ代表: 在數學中的黎曼ζ函式和其他的ζ函式 聚合物力學的黏性...
Β分布的機率密度函式是:其中 是Γ函式。隨機變數X服從參數為 的Β分布通常寫作Β分布累積分布函式 Β分布的累積分布函式是:其中 是不完全Β函式, 是正則不完全...
這裡給出狄利克雷分布的機率密度函式、邊緣分布與聯合分布的推導。...式中 表示雙伽瑪函式(Digamma function),即Gamma函式的對數導數。...
(2)作為階乘延拓的伽瑪函式是定義在複數範圍內的亞純函式,與之有密切聯繫的函式還有貝塔函式(他們分別被稱為歐拉第二積分與歐拉第一積分)。 拿伽瑪函式 來說,顯...
