基本介紹
- 中文名:伽瑪分布
- 外文名:Gamma distribution
- 領域:統計學
- 參數:形狀參數,尺度參數
- 特例:指數分布,卡方分布
- 類型:連續性機率分布
定義
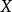

若干性質及證明















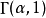






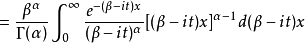




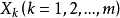









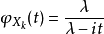









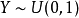









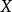
















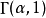






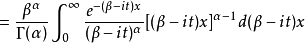




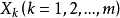









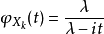









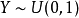








伽瑪分布是統計學中的一種連續機率函式,包含兩個參數α和β,其中α稱為形狀參數,β稱為尺度參數。...
伽瑪分布(Gamma Distribution)是統計學的一種連續機率函式,是機率統計中一種非常重要的分布。“指數分布”和“χ2分布”都是伽馬分布的特例。Gamma分布中的參數α稱...
伽瑪函式(Gamma函式),也叫歐拉第二積分,是階乘函式在實數與複數上擴展的一類函式。該函式在分析學、機率論、偏微分方程和組合數學中有重要的套用。與之有密切聯繫...
分布參數A服從伽瑪分布的複合泊松分布。 ...... 分布參數A服從伽瑪分布的複合泊松分布。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,...
連續分布( continuous distribution)連續型隨機變數X的分布函式是連續的,它對應的分布為連續分布。常用的連續分布有常態分配、均勻分布、指數分布、伽瑪分布、貝塔分布...
貝塔分布(Beta Distribution) 是一個作為伯努利分布和二項式分布的共軛先驗分布的密度函式,在機器學習和數理統計學中有重要套用。在機率論中,貝塔分布,也稱Β分布,是...
壽命分布(life distribution)可靠性統計的基本概念之一它是壽命這個隨機變數的分布.常用其分布函式 表示.常用的壽命分布有指數分布、威布爾分布、對數正態分布、伽瑪...
伽馬高度表是指用伽馬γ射線量相對地面高度的裝置。它是一個裝有γ源的設備,...1. 袁祖貴.採用自然伽馬能譜測井儀研究天然放射性元素的高度和深度分布規律[J]...
如果不將圖像進行伽馬編碼,那么數據位或者頻寬的利用就會分布不均勻——會有過多的數據位或者頻寬用來表示人類根本無法察覺到的差異,而用於表示人類非常敏感的視覺感知...
在貝葉斯統計中,如果後驗分布與先驗分布屬於同類,則先驗分布與後驗分布被稱為共軛分布,而先驗分布被稱為似然函式的共軛先驗。...
在機率論中,Β分布也稱貝塔分布,是指一組定義在 (0,1)區間的連續機率分布。...... 其中 表示雙伽瑪函式。聯合熵為:其KL散度為:參考資料 1. On the entropy ...
韋布爾分布,即韋伯分布(Weibull distribution),又稱韋氏分布或威布爾分布,是可靠性分析和壽命檢驗的理論基礎。威布爾分布在可靠性工程中被廣泛套用,尤其適用於機電類...
伽瑪值指印刷技術或圖象處理上,輸入值和顯示器輸出時的亮度之間的關係,其影響原稿上高光到暗調之間色調的分布。...
伽瑪刀(Gamma Knife)是立體定向放射外科(Stereotactic Radiosurgery)的主要治療手段,是根據立體幾何定向原理, 將顱內的正常組織或病變組織選擇性地確定為靶點,使用鈷-...
放射性核素比活度測量用多道伽瑪能譜儀分析。能譜儀要用標準源(多能量峰或者混合源)進行能量和效率刻度,刻度源體積、形狀和待測樣品一致。必要時,效率刻度要符合...
伽瑪照相機,又稱γ照相機、閃爍照相機,是用來給釋放γ輻射的輻射核素進行成像的一種醫療器械。在早期藥物開發和核醫療成像中廣泛套用,可以用來分析人體和放射性標記...
伽瑪分布(以Γ函式定義的連續機率分布) 第二種的克氏符號 圖中與一頂點中有邊相連的頂點 γ代表: 結構工程中負荷與材質的安全係數 物質的比重量 下不...
幾年觀測下來,科學家發現伽馬射線暴出現在天空的各個方向上,而這就與星系或類星體的分布很相似,而這與銀河系內天體的分布完全不一樣。於是,人們開始認真看待...
